题目内容
若函数f（x）=x3-3x+a有两个不同的零点，则实数a的取值是 ．
考点：函数的零点与方程根的关系,利用导数研究函数的极值
专题：函数的性质及应用
分析：利用导数求出函数的极大值和极小值，要使函数f（x）=x3-3x+a只有2个零点，则满足极大值等于0或极小值等于0．
解答：
解：：∵f（x）=x3-3x+a，∴f'（x）=3x2-3，
由f'（x）＞0，得x＞1或x＜-1，此时函数单调递增，
由f'（x）＜0，得-1＜x＜1，此时函数单调递减．
即当x=-1时，函数f（x）取得极大值，当x=1时，函数f（x）取得极小值．
要使函数f（x）=x3-3x+a只有两个零点，则满足极大值等于0或极小值等于0，
由极大值f（-1）=-1+3+a=a+2=0，解得a=-2；再由极小值f（1）=1-3+m=a-2=0，解得a=2．
综上实数m的取值范围：a=-2或a=2，
故答案为-2或2．
由f'（x）＞0，得x＞1或x＜-1，此时函数单调递增，
由f'（x）＜0，得-1＜x＜1，此时函数单调递减．
即当x=-1时，函数f（x）取得极大值，当x=1时，函数f（x）取得极小值．
要使函数f（x）=x3-3x+a只有两个零点，则满足极大值等于0或极小值等于0，
由极大值f（-1）=-1+3+a=a+2=0，解得a=-2；再由极小值f（1）=1-3+m=a-2=0，解得a=2．
综上实数m的取值范围：a=-2或a=2，
故答案为-2或2．
点评：本题主要考查三次函数的图象和性质，利用导数求出函数的极值是解决本题的关键，属于中档题．
练习册系列答案
相关题目
设a=50.3，b=0.35，c=log50.3+log52，则a，b，c的大小关系是（ ）
| A、b＜c＜a |
| B、a＜b＜c |
| C、c＜a＜b |
| D、c＜b＜a |
过椭圆C：
+
=1上任一点P，作椭圆C的右准线的垂线PH（H为垂足），延长PH到点Q，使|HQ|=λ|PH|（λ≥1）．当点P在椭圆C上运动时，点Q的轨迹的离心率的取值范围为（ ）
| x2 |
| 3 |
| y2 |
| 2 |
A、（0，
| ||||||||
B、（
| ||||||||
C、[
| ||||||||
D、（
|
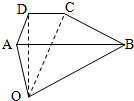如图，梯形ABCD中AB∥CD，AB=2CD，点O为空间任意一点，设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|