题目内容
 在三棱锥A-BCD中,AB⊥AC,AB⊥AD,AC⊥AD,AB=AC=1,AD=2,E、F分别是BC、BD的中点.
在三棱锥A-BCD中,AB⊥AC,AB⊥AD,AC⊥AD,AB=AC=1,AD=2,E、F分别是BC、BD的中点.(1)求证:BC⊥面AED;
(2)求A到面BCD的距离;
(3)求二面角C-AE-F的大小.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由于E是BC的中点,利用等腰三角形的性质可得AE⊥BC.再利用三垂线定理可得BC⊥DE.利用线面垂直的判定定理就看得出.
(2)利用“等积变形”即可得出;
(3)通过建立空间直角坐标系,利用两角平面的法向量的夹角公式即可得出二面角的平面角.
(2)利用“等积变形”即可得出;
(3)通过建立空间直角坐标系,利用两角平面的法向量的夹角公式即可得出二面角的平面角.
解答:
(1)证明:∵AB=AC=1,E是BC的中点,
∴AE⊥BC,
又∵AB⊥AD,AC⊥AD,AB∩AC=A.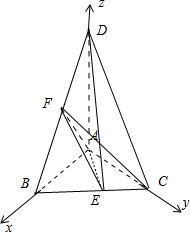
∴AD⊥平面ABC.
∴BC⊥DE.
∵AE∩DE=E,∴BC⊥面AED.
(2)∵VA-BCD=
×
×1×2=
,S△BCD=
BC×DE=
×
=
,
设A到面BCD的距离为h,∴
S△BCD•h=
.解得h=
.
∴h=
.
(3)建立如图所示的空间直角坐标系.则A(0,0,0),B(1,0,0),C(0,1,0),D(0,0,2),E(
,
,0),F(
,0,1).
则
=(
,0,1),
=(
,
,0).
设平面AEF的法向量为
=(x,y,z),则
,令z=-1,解得x=2,y=-2.
∴
=(2,-2,-1).
可取平面ACE的法向量为
=(0,0,1).则cos<
,
>=
=
=-
.
从图中看到:二面角C-AE-F的平面角是钝角,
∴二面角C-AE-F的大小为π-arccos
.
∴AE⊥BC,
又∵AB⊥AD,AC⊥AD,AB∩AC=A.

∴AD⊥平面ABC.
∴BC⊥DE.
∵AE∩DE=E,∴BC⊥面AED.
(2)∵VA-BCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
5-
|
| 3 |
| 2 |
设A到面BCD的距离为h,∴
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
∴h=
| 2 |
| 3 |
(3)建立如图所示的空间直角坐标系.则A(0,0,0),B(1,0,0),C(0,1,0),D(0,0,2),E(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则
| AF |
| 1 |
| 2 |
| AE |
| 1 |
| 2 |
| 1 |
| 2 |
设平面AEF的法向量为
| n |
|
∴
| n |
可取平面ACE的法向量为
| m |
| m |
| n |
| ||||
|
|
| -1 | ||
|
| 1 |
| 3 |
从图中看到:二面角C-AE-F的平面角是钝角,
∴二面角C-AE-F的大小为π-arccos
| 1 |
| 3 |
点评:熟练掌握等腰三角形的性质、三垂线定理、线面垂直的判定定理、“等积变形”、通过建立空间直角坐标系,利用两角平面的法向量的夹角公式求出二面角的平面角等是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
过椭圆C:
+
=1上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1).当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )
| x2 |
| 3 |
| y2 |
| 2 |
A、(0,
| ||||||||
B、(
| ||||||||
C、[
| ||||||||
D、(
|
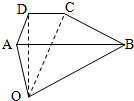 如图,梯形ABCD中AB∥CD,AB=2CD,点O为空间任意一点,设
如图,梯形ABCD中AB∥CD,AB=2CD,点O为空间任意一点,设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.