题目内容
已知函数f(x)=x2-4sinθ•x-1,x∈[-1,
],其中θ∈[0,2π]
(1)当θ=
时,求函数f(x)的最大最小值;
(2)求θ的取值范围,使y=f(x)在区间[-1,
]上存在反函数.
| 3 |
(1)当θ=
| π |
| 6 |
(2)求θ的取值范围,使y=f(x)在区间[-1,
| 3 |
考点:二次函数在闭区间上的最值,反函数
专题:计算题,函数的性质及应用
分析:(1)把θ=
代入可得函数解析式,由二次函数区间的最值可得;
(2)可得函数的图象为开口向上的抛物线,对称轴为x=2sinθ,要满足题意须使函数在该区间单调,可得 2sinθ≤-1,或2sinθ≥
,解之可得.
| π |
| 6 |
(2)可得函数的图象为开口向上的抛物线,对称轴为x=2sinθ,要满足题意须使函数在该区间单调,可得 2sinθ≤-1,或2sinθ≥
| 3 |
解答:
解:(1)当θ=
时,f(x)=x2-2x-1=(x-1)2-2,
函数的图象为开口向上的抛物线,对称轴为x=1,
故当x∈[-1,1]时,函数单调递减,
当x∈[1,
]时,函数单调递增,
故当x=1时,函数取最小值f(1)=-2,
当x=-1时,函数取最大值f(-1)=2;
(2)可得f(x)=(x-2sinθ)2-1-4sin2θ,
函数的图象为开口向上的抛物线,对称轴为x=2sinθ,
要使函数y=f(x)在区间[-1,
]上存在反函数,
必须使函数在该区间单调,故2sinθ≤-1,或2sinθ≥
,
可得sinθ≤-
,或sinθ≥
,
解之可得
≤θ≤
,或
≤θ≤
,
故θ的取值范围为:
≤θ≤
,或
≤θ≤
| π |
| 6 |
函数的图象为开口向上的抛物线,对称轴为x=1,
故当x∈[-1,1]时,函数单调递减,
当x∈[1,
| 3 |
故当x=1时,函数取最小值f(1)=-2,
当x=-1时,函数取最大值f(-1)=2;
(2)可得f(x)=(x-2sinθ)2-1-4sin2θ,
函数的图象为开口向上的抛物线,对称轴为x=2sinθ,
要使函数y=f(x)在区间[-1,
| 3 |
必须使函数在该区间单调,故2sinθ≤-1,或2sinθ≥
| 3 |
可得sinθ≤-
| 1 |
| 2 |
| ||
| 2 |
解之可得
| 7π |
| 6 |
| 11π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
故θ的取值范围为:
| 7π |
| 6 |
| 11π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
点评:本题考查二次函数区间的最值,涉及三角函数和反函数的应用,属中档题.

练习册系列答案
相关题目
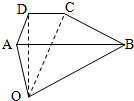 如图,梯形ABCD中AB∥CD,AB=2CD,点O为空间任意一点,设
如图,梯形ABCD中AB∥CD,AB=2CD,点O为空间任意一点,设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
已知x1>0,x1≠1且xn+1=
(n=1,2,…),试证:“数列{xn}对任意的正整数n,都满足xn>xn+1,”当此题用反证法否定结论时应为( )
xn•(
| ||
3
|
| A、对任意的正整数n,有xn=xn+1 |
| B、存在正整数n,使xn≤xn+1 |
| C、存在正整数n,使xn≥xn-1,且xn≥xn+1 |
| D、存在正整数n,使(xn-xn-1)(xn-xn+1)≥0 |
 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.