题目内容
(1)已知圆C的参数方程为
(α为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsinθ=1,(ρ≥0,0≤θ<2π)则直线l与圆C的交点的极坐标为 .
(2)已知f(x)=|x|+|x-1|,若g(x)=f(x)-a的零点个数不为0,则a的最小值为 .
|
(2)已知f(x)=|x|+|x-1|,若g(x)=f(x)-a的零点个数不为0,则a的最小值为
考点:函数的零点
专题:函数的性质及应用,直线与圆
分析:(1)先根据同角三角函数关系消去参数α,求出圆的标准方程,再根据直线的极坐标方程求出直线的普通方程,然后联立圆的方程与直线方程求出交点坐标即可;
(2)根据g(x)=f(x)-a的零点个数不为0,即方程a=f(x)有解,转化为求函数f(x)=|x|+|x-1|的值域,利用绝对值不等式的几何意义即可求得结果.
(2)根据g(x)=f(x)-a的零点个数不为0,即方程a=f(x)有解,转化为求函数f(x)=|x|+|x-1|的值域,利用绝对值不等式的几何意义即可求得结果.
解答:
解:(1)由题设知,在直角坐标系下,直线l的方程为y=1,圆C的方程为x2+(y-1)2=1.
又解方程组
,
得
或
.
故所求交点的直角坐标为(-1,1),(1,1).
故直线l与圆C的交点的极坐标为(
,
),(
,
)
(2)由绝对值不等式的几何意义知:
f(x)=|x|+|x-1|≥1;
若g(x)=f(x)-a的零点个数不为0,
即方程a=f(x)有解,因此a≥1.
故a的最小值为1
故答案为 (1)(
,
),(
,
);(2)1
又解方程组
|
得
|
|
故所求交点的直角坐标为(-1,1),(1,1).
故直线l与圆C的交点的极坐标为(
| 2 |
| π |
| 4 |
| 2 |
| 3π |
| 4 |
(2)由绝对值不等式的几何意义知:
f(x)=|x|+|x-1|≥1;
若g(x)=f(x)-a的零点个数不为0,
即方程a=f(x)有解,因此a≥1.
故a的最小值为1
故答案为 (1)(
| 2 |
| π |
| 4 |
| 2 |
| 3π |
| 4 |
点评:(1)本题主要考查了圆的参数方程,以及直线与圆的方程的应用,属于基础题.
(2)此题是基础题.考查函数的零点与函数图象的交点之间的关系,体现了转化的能力,同时考查了学生灵活应用知识分析解决问题的能力和计算能力.
(2)此题是基础题.考查函数的零点与函数图象的交点之间的关系,体现了转化的能力,同时考查了学生灵活应用知识分析解决问题的能力和计算能力.

练习册系列答案
相关题目
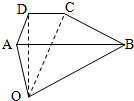 如图,梯形ABCD中AB∥CD,AB=2CD,点O为空间任意一点,设
如图,梯形ABCD中AB∥CD,AB=2CD,点O为空间任意一点,设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
为了考察甲、乙两种小麦的长势,分别从中抽取了10株苗,测得苗高如下(单位:cm):
甲:12,13,14,15,10,16,13,11,5,11;
乙:8,16,15,14,13,11,10,11,10,12;
则下列说法正确的是( )
甲:12,13,14,15,10,16,13,11,5,11;
乙:8,16,15,14,13,11,10,11,10,12;
则下列说法正确的是( )
| A、甲的平均苗高比乙 |
| B、乙的平均苗高比甲高 |
| C、平均苗高一样,甲长势整齐 |
| D、平均苗高一样,乙长势整齐 |
 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.