题目内容
已知
，
是互相垂直的单位向量，设
=4
+3
，
=3
-4
，则
•
= ．
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
考点：平面向量数量积的性质及其运算律
专题：平面向量及应用
分析：利用向量数量积得坐标运算法则即可得出．
解答：
解：∵
=4
+3
=（4，3），
=3
-4
=（3，-4），
∴
•
=4×3+3×（-4）=0．
故答案为0．
| a |
| i |
| j |
| b |
| i |
| j |
∴
| a |
| b |
故答案为0．
点评：熟练掌握向量数量积得坐标运算法则是解题的关键．
练习册系列答案
相关题目
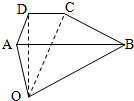如图，梯形ABCD中AB∥CD，AB=2CD，点O为空间任意一点，设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
已知x1＞0，x1≠1且xn+1=
（n=1，2，…），试证：“数列{xn}对任意的正整数n，都满足xn＞xn+1，”当此题用反证法否定结论时应为（ ）
xn•(
| ||
3
|
| A、对任意的正整数n，有xn=xn+1 |
| B、存在正整数n，使xn≤xn+1 |
| C、存在正整数n，使xn≥xn-1，且xn≥xn+1 |
| D、存在正整数n，使（xn-xn-1）（xn-xn+1）≥0 |