题目内容
已知实数x,y满足不等式
,则
的取值范围是 .
|
| 2x3+y3 |
| x2y |
考点:简单线性规划的应用
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,设目标函数为z=
=
+(
)2,通过换元法设t=
,则利用导数求函数的最值.
| 2x3+y3 |
| x2y |
| 2x |
| y |
| y |
| x |
| y |
| x |
解答:
解:由条件知可行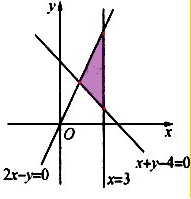 域是由点(3,6),(3,1),(
域是由点(3,6),(3,1),(
,
),为顶点组成的三角形及其内部,
设z=
=
+(
)2,其中(
)min=
,(
)max=2,
设t=
,则z=f(t)=t2+
,∴f'(t)=2t-
=
,其中t∈[
,2],
当
≤t<1时,f'(t)>0,函数f(t)单调递增,当1<t≤2时,f'(t)<0,函数f(t)单调递减,∴当t=1时,f(t)min=f(1)=3.
又f(
)=
,f(2)=5,故f(t) max=
,即所求取值范围是[3,
].
故答案为:[3,
].
 域是由点(3,6),(3,1),(
域是由点(3,6),(3,1),(| 4 |
| 3 |
| 8 |
| 3 |
设z=
| 2x3+y3 |
| x2y |
| 2x |
| y |
| y |
| x |
| y |
| x |
| 1 |
| 3 |
| y |
| x |
设t=
| y |
| x |
| 2 |
| t |
| 2 |
| t2 |
| 2(t3-1) |
| t2 |
| 1 |
| 3 |
当
| 1 |
| 3 |
又f(
| 1 |
| 3 |
| 55 |
| 9 |
| 55 |
| 9 |
| 55 |
| 9 |
故答案为:[3,
| 55 |
| 9 |
点评:本题主要考查线性规划的应用,注意本题不能直接将三点坐标代入目标函数求其取值范围,否则容易出错.

练习册系列答案
相关题目
设a=50.3,b=0.35,c=log50.3+log52,则a,b,c的大小关系是( )
| A、b<c<a |
| B、a<b<c |
| C、c<a<b |
| D、c<b<a |
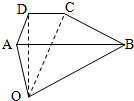 如图,梯形ABCD中AB∥CD,AB=2CD,点O为空间任意一点,设
如图,梯形ABCD中AB∥CD,AB=2CD,点O为空间任意一点,设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.