题目内容
19.若实数x,y满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$,则2x+y的最小值为$-\frac{1}{2}$.分析 作出不等式组对应的平面区域,利用z的几何意义,即可得到结论.
解答 解:作出不等式组对应的平面区域如图:
由z=2x+y得y=-2x+z,
平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点A时,直线的截距最小,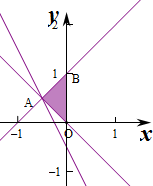
此时z最小,
由$\left\{\begin{array}{l}{x-y+1=0}\\{x+y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{1}{2}}\end{array}\right.$,
即A(-$\frac{1}{2}$,$\frac{1}{2}$),此时z=-$\frac{1}{2}$×2+$\frac{1}{2}$=-$\frac{1}{2}$,
故答案为:$-\frac{1}{2}$.
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
9.四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程和相关系数r,分别得到以下四个结论:
①y=2.35x-6.42,r=-0.93 ②y=-3.47x+5.65,r=-0.95
③y=5.43x+8.49,r=0.98 ④y=-4.32x-4.58,r=0.89
其中,一定不正确的结论序号是( )
①y=2.35x-6.42,r=-0.93 ②y=-3.47x+5.65,r=-0.95
③y=5.43x+8.49,r=0.98 ④y=-4.32x-4.58,r=0.89
其中,一定不正确的结论序号是( )
| A. | ②③ | B. | ①④ | C. | ①②③ | D. | ②③④ |
7.设loga$\frac{2}{3}$>1,则实数a的取值范围是( )
| A. | 0<a<$\frac{2}{3}$ | B. | $\frac{2}{3}$<a<1 | C. | 0<a<$\frac{2}{3}$或a>1 | D. | a>$\frac{2}{3}$ |
4.已知$\overrightarrow{a}$=(1,$\sqrt{3}$),b=($\sqrt{3}$,k),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则k=( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
5.椭圆b2x2+a2y2=1(a>b>0)的左焦点为F,右顶点为A,上顶点为B,若∠ABF=90°,则椭圆的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |