题目内容
10.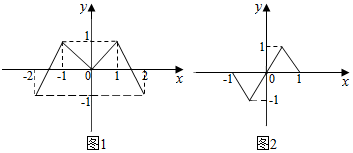 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )| A. | 3 | B. | 7 | C. | 10 | D. | 14 |
分析 由f(x)和g(x)的图象便可看出f(g(x))=0时可得到g(x)=0,而由g(x)的图象即可看出g(x)=0的实根个数为3,从而便得出方程f(g(x))=0的实根个数a=3,而用同样的方法可以求出方程g(f(x))=0的实根个数b的值,从而得出a+b的值.
解答 解:由f(x),g(x)的图象和f(g(x))=0得:g(x)=0;
∴x=-1,0,1,即a=3;
由g(f(x))=0得,f(x)=0,-1,或1;
∴由f(x)的图象可看出f(x)=0的实根有3个,f(x)=-1的实根有2个,f(x)=1的实根有2个;
∴b=3+2+2=7;
∴a+b=10.
故选:C.
点评 考查奇函数、偶函数的定义,以及根据图象求方程实数根个数的方法,清楚函数f(x)的图象和x轴交点与方程f(x)=0实根的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.如果执行如所示的程序框图,那么输出的S=( )


| A. | 119 | B. | 600 | C. | 719 | D. | 4949 |
15. 为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
测试成绩(单位:次/分钟)如表:
(Ⅰ)补全茎叶图并指出乙队测试成绩的中位数和众数;
(Ⅱ)试用统计学中的平均数、方差知识对甲乙两个代表队的测试成绩进行分析.
 为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,测试成绩(单位:次/分钟)如表:
| 轮次 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲 | 73 | 66 | 82 | 72 | 63 | 76 |
| 乙 | 83 | 75 | 62 | 69 | 75 | 68 |
(Ⅱ)试用统计学中的平均数、方差知识对甲乙两个代表队的测试成绩进行分析.
19.在复平面内,复数(1+$\sqrt{3}$i)•i对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.已知圆C:x2+y2-4x=0,直线l:kx-3k-y=0,则直线l与圆C的位置关系是( )
| A. | 相交 | B. | 相切 | ||
| C. | 相离 | D. | 以上三种均有可能 |