题目内容
20．已知椭圆$\frac{{x}^{2}}{10-m}$+$\frac{{y}^{2}}{m-2}$=1，焦点在x轴上，若焦距为4，则m等于（ ）| A． | 4 | B． | 5 | C． | 4或8 | D． | 5或7 |
分析 由题意可得c=2，10-m-（m-2）=4，解方程即可得到所求值．
解答 解：由题意可得10-m＞m-2＞0，
可得2＜m＜6，
又2c=4，即有c=2，
可得10-m-（m-2）=4，
解得m=4．
故选：A．
点评 本题考查椭圆的方程和性质，考查椭圆的基本量的关系，考查运算能力，属于基础题．
练习册系列答案
相关题目
11．设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1，F2，离心率为e，过F2的直线与椭圆的交于A，B两点，若△F1AB是以A为顶点的等腰直角三角形，则e2=（ ）
| A． | 3-2$\sqrt{2}$ | B． | 5-3$\sqrt{2}$ | C． | 9-6$\sqrt{2}$ | D． | 6-4$\sqrt{2}$ |
8．已知$α∈（\frac{π}{2}，π）$，且sin（π+α）=-$\frac{3}{5}$，则tanα=（ ）
| A． | $-\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{4}$ | D． | $-\frac{4}{3}$ |
15．倾斜角为60°的直线l过抛物线y2=4x的焦点F，且与抛物线位于x轴上的部分相交于A，则△OFA的面积为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\sqrt{3}$ | D． | $2\sqrt{3}$ |
5．变量x，y满足约束条件$\left\{\begin{array}{l}x+y-2≥0\\ x-y-2≤0\\ y≥1\end{array}\right.$，则目标函数z=x+3y的最小值为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
12．
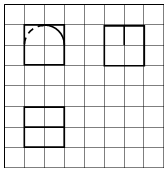如图所示，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某几何体的三视图（其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧），则该几何体的体积为（ ）
如图所示，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某几何体的三视图（其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧），则该几何体的体积为（ ）| A． | $6+\frac{π}{4}$ | B． | $6+\frac{π}{2}$ | C． | $6-\frac{π}{4}$ | D． | $6-\frac{π}{2}$ |
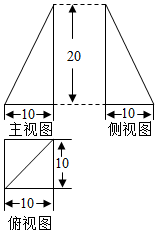董师傅用铁皮制作一封闭的工件，且三视图如图所示（单位：cm），图中水平线与竖直线垂直），则制作该工件用去的铁皮的面积为（制作过程铁皮的损耗忽略不计）（100（3+$\sqrt{5}$）cm2．
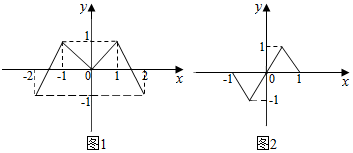已知偶函数f（x），奇函数g（x）的图象分别如图（1）、图（2）所示，方程f（g（x））=0，g（f（x））=0的实根的个数分别为a，b，则a+b=（ ）