题目内容
15. 为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,测试成绩(单位:次/分钟)如表:
| 轮次 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲 | 73 | 66 | 82 | 72 | 63 | 76 |
| 乙 | 83 | 75 | 62 | 69 | 75 | 68 |
(Ⅱ)试用统计学中的平均数、方差知识对甲乙两个代表队的测试成绩进行分析.
分析 (Ⅰ)根据题意补全茎叶图,求出乙队测试成绩的中位数与众数;
(Ⅱ)求出甲、乙二人的平均数与方差,进行比较即可.
解答 解:(Ⅰ)画出茎叶图如下: …(4分)
…(4分)
乙队测试成绩的中位数为72,众数为75.…(6分)
(Ⅱ)$\overline{{x}_{甲}}$=$\frac{63+66+72+73+76+82}{6}$=72,
${{s}_{甲}}^{2}$=$\frac{1}{6}[(63-72)2+(66-72)2+(72-72)2+(73-72)2+(76-72)2+(82-72)2]$=39;
$\overline{{x}_{乙}}$=$\frac{62+68+69+75+75+83}{6}$=72,
${{s}_{乙}}^{2}$=$\frac{1}{6}[(62-72)2+(68-72)2+(69-72)2+(75-72)2+(75-72)2+(83-72)2]$=44,…(10分)
因为$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${{s}_{甲}}^{2}$<${{s}_{乙}}^{2}$,所以甲乙两队水平相当,但甲队发挥较稳定.…(12分)
点评 本题考查了茎叶图的应用问题,也考查了平均数与方差的应用问题,是基础题目.

练习册系列答案
相关题目
5.变量x,y满足约束条件$\left\{\begin{array}{l}x+y-2≥0\\ x-y-2≤0\\ y≥1\end{array}\right.$,则目标函数z=x+3y的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
7.设集合S={1,2,…,2016},若X是S的子集,把X中所有元素之和称为X的“容量”,(规定空集容量为0),若X的容量为奇(偶)数,则称X为S的奇(偶)子集,记S的奇子集个数为m,偶子集个数为n,则m,n之间的关系为( )
| A. | m=n | B. | m>n | C. | m<n | D. | 无法确定 |
4.阅读如图所示的程序框图,运行相应的程序,若判断框内是n≤6,则输出的S为( )
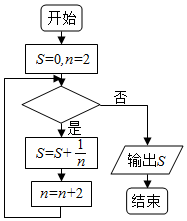

| A. | $\frac{3}{4}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{5}{6}$ |
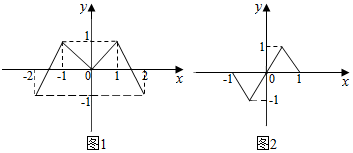 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )