题目内容
5.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点是(-$\sqrt{3}$,0)、($\sqrt{3}$,0),且椭圆经过点($\sqrt{2}$,$\frac{\sqrt{2}}{2}$).(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A,B两点,且以AB为直径的圆过椭圆右顶点M,求证:直线l恒过定点.
分析 (1)设出椭圆方程,由题意可得a2-b2=3,再由椭圆的定义可得2a=4,解得a=2,b=1,进而得到椭圆方程;
(2)由题意可知,直线l的斜率为0时,不合题意.不妨设直线l的方程为x=ky+m,代入椭圆方程,消去x,运用韦达定理和由题意可得MA⊥MB,向量垂直的条件:数量积为0,化简整理,可得m=$\frac{6}{5}$或m=2,即可得到定点.
解答 解:(1)椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,
由题意可得c=$\sqrt{3}$,
∴a2-b2=3,
由$2a=\sqrt{{{(\sqrt{2}+\sqrt{3})}^2}+\frac{1}{2}}+\sqrt{{{(\sqrt{2}-\sqrt{3})}^2}+\frac{1}{2}}=\sqrt{\frac{11}{2}+2\sqrt{6}}+\sqrt{\frac{11}{2}-2\sqrt{6}}=4$,
可得a=2,b=1,
所求椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$;
(2)证明:由题意可知,直线l的斜率为0时,不合题意.
不妨设直线l的方程为x=ky+m.
由$\left\{\begin{array}{l}{x=ky+m}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,
消去x得(4+k2)y2+2kmy+m2-4=0.
设A(x1,y1),B(x2,y2),则有y1+y2=-$\frac{2km}{{k}^{2}+4}$…①,y1y2=$\frac{{m}^{2}-4}{{k}^{2}+4}$…②
因为以AB为直径的圆过点M,所以$\overrightarrow{MA}$•$\overrightarrow{MB}$=0.
由$\overrightarrow{MA}$=(x1-2,y1),$\overrightarrow{MB}$=(x2-2,y2),得(x1-2)(x2-2)+y1y2=0.
将x1=ky1+m,x2=ky2+m代入上式,
得(k2+1)y1y2+k(m-2)(y1+y2)+(m-2)2=0…③
将①②代入③,得 $\frac{5{m}^{2}-16m+12}{{k}^{2}+4}$=0,解得m=$\frac{6}{5}$或m=2(舍).
综上,直线l经过定点($\frac{6}{5}$,0).
点评 本题考查椭圆的方程的求法,注意运用椭圆的定义,考查直线恒过定点的求法,注意联立直线方程和椭圆方程,运用韦达定理和向量垂直的条件:数量积为0,考查运算能力,属于中档题.

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{5}{3}$ | D. | 4 |
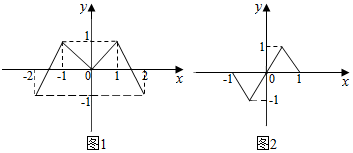 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )