题目内容
函数f（x）=-x2+ax+3，在（-∞，1]上是增函数，则a的取值范围是 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：先求出二次函数的对称轴，由区间（-∞，1]在对称轴的左侧，列出不等式解出a的取值范围．
解答：
解：∵函数f（x）=-x2+ax+3在区间（-∞，1]上是增函数，
对称轴为 x=
，
∴区间（-∞，1]在对称轴的左侧，
∴
≥1，
∴a≥2，
则a的取值范围为[2，+∞）
故答案为：[2，+∞）
对称轴为 x=
| a |
| 2 |
∴区间（-∞，1]在对称轴的左侧，
∴
| a |
| 2 |
∴a≥2，
则a的取值范围为[2，+∞）
故答案为：[2，+∞）
点评：本题考查二次函数图象特征和单调性，以及不等式的解法．
练习册系列答案
相关题目
某三棱锥的三视图如图所示，则这个三棱锥的体积为(
-
)8二项展开式中的常数项为（ ）
| 3 | x |
| 2 |
| x |
| A、56 | B、112 |
| C、-56 | D、-112 |
已知圆C的圆心是直线x-y+1=0与x轴的交点，且圆C与直线x+y+3=0相切，则圆C的方程是（ ）
| A、（x+1）2+y2=2 |
| B、（x+1）2+y2=8 |
| C、（x-1）2+y2=2 |
| D、（x-1）2+y2=8 |
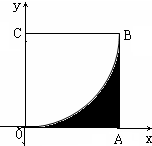如图，已知正方形OABC的四个顶点坐标分别为O（0，0），A（1，0），B（1，1），C（0，1），现向该正方体内部随机投1000个点，统计出所投点落在阴影部分的个数为328，由此估计图中阴影部分的面积为（ ）