题目内容
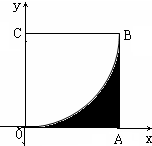如图，已知正方形OABC的四个顶点坐标分别为O（0，0），A（1，0），B（1，1），C（0，1），现向该正方体内部随机投1000个点，统计出所投点落在阴影部分的个数为328，由此估计图中阴影部分的面积为（ ）| A、0.328 | B、0.672 |
| C、0.3 | D、0.7 |
考点：几何概型
专题：概率与统计
分析：根据几何概型的概率公式，可以求出豆子落在阴影部分的概率，然后即可得到阴影部分的面积．
解答：
解：向该正方体内部随机投1000个点，统计出所投点落在阴影部分的个数为328，
则豆子落在阴影部分的概率P=
=0.328，
∵正方形OABC的四个顶点坐标分别为O（0，0），A（1，0），B（1，1），C（0，1），
∴正方形的面积为1，
设阴影部分的面积S，满足
=0.328，即S=0.328，
故选：A
则豆子落在阴影部分的概率P=
| 328 |
| 1000 |
∵正方形OABC的四个顶点坐标分别为O（0，0），A（1，0），B（1，1），C（0，1），
∴正方形的面积为1，
设阴影部分的面积S，满足
| S |
| 1 |
故选：A
点评：本题主要考查几何概型的应用，根据面积之间的关系是解决本题的关键，比较基础．
练习册系列答案
相关题目
某社区四支篮球队参加比赛，现任意将这四支队分成两个组（每组两个队）进行比赛，胜者再赛，则所有可能的比赛情况共有（ ）
| A、3种 | B、6种 |
| C、12种 | D、24种 |
已知k∈[-2，2]，则k的值使得过点A（0，2）可以作2条直线与圆x2+y2+kx-2y+
k=0相切的概率为（ ）
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若sin（
-α）=
，则cos（
+2α）=（ ）
| π |
| 6 |
| 1 |
| 3 |
| 2π |
| 3 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
二项式（x2-
）11的展开式中，系数最大的项为（ ）
| 1 |
| x |
| A、第五项 | B、第六项 |
| C、第七项 | D、第六和第七项 |