题目内容
已知球面面积为16π,A、B、C为球面上三点,且AB=2,BC=1,AC=
,则球心到平面ABC的距离为 .
| 3 |
考点:球面距离及相关计算
专题:计算题,球
分析:由球面面积为16π,根据球的表面积公式,易求出球的半径为2;又由AB=2,BC=1,AC=
,我们易判断出△ABC为以C为直角的直角三角形,根据直角三角形外接圆半径等于斜边的一半,我们可以求出截面的半径,再根据球心距、截面圆半径、球半径构成直角三角形,满足勾股定理,我们易得球心O到平面ABC的距离.
| 3 |
解答:
解:∵球面面积S=16π=4πR2,
∴R2=4
∴R=2
∵AB=2,BC=1,AC=
,
∴△ABC为以C为直角的直角三角形
∴平面ABC截球得到的截面圆半径r=
AB=1
∴球心O到平面ABC的距离d=
=
.
故答案为:
.
∴R2=4
∴R=2
∵AB=2,BC=1,AC=
| 3 |
∴△ABC为以C为直角的直角三角形
∴平面ABC截球得到的截面圆半径r=
| 1 |
| 2 |
∴球心O到平面ABC的距离d=
| R2-r2 |
| 3 |
故答案为:
| 3 |
点评:球的截面圆半径为r,球心距为d,球半径为R,则球心距、截面圆半径、球半径构成直角三角形,满足勾股定理,即R2=r2+d2.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
二项式(x2-
)11的展开式中,系数最大的项为( )
| 1 |
| x |
| A、第五项 | B、第六项 |
| C、第七项 | D、第六和第七项 |
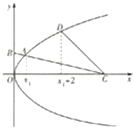 抛物线M:y2=2px(p>0)的准线过椭圆N:
抛物线M:y2=2px(p>0)的准线过椭圆N: