题目内容
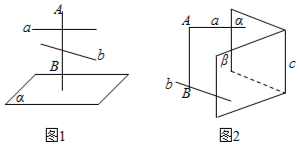
5．
把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C，（其中BD=2AD，BC=AC）则异面直线DC，AB所成角的正切值为（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{7}$ | C． | $\frac{{\sqrt{21}}}{7}$ | D． | $\frac{{\sqrt{21}}}{3}$ |
分析 以A为原点，AB、AD所在直线分别为y轴和x轴，建立空间直角坐标系，利用向量法能求出异面直线DC，AB所成角的正切值．
解答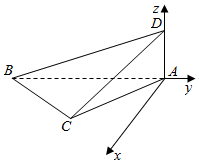 
解：以A为原点，AB、AD所在直线分别为y轴和x轴，建立如图坐标系
Rt△ABD中，AD：AB：BD=1：$\sqrt{3}$：2，
Rt△ABC中，AC：AB：BC=1：$\sqrt{2}$：1，
设AD=$\sqrt{2}$，则AB=$\sqrt{6}$，BC=AC=$\sqrt{3}$，
则A（0，0，0），B（0，-$\sqrt{6}$，0），C（$\frac{\sqrt{6}}{2}$，-$\frac{\sqrt{6}}{2}$，0），D（0，0，$\sqrt{2}$），
∴$\overrightarrow{AB}$=（0，-$\sqrt{6}$，0），$\overrightarrow{DC}$=（$\frac{\sqrt{6}}{2}$，-$\frac{\sqrt{6}}{2}$，-$\sqrt{2}$），
设异面直线DC，AB所成角为θ，
则cosθ=$\frac{|\overrightarrow{AB}•\overrightarrow{DC}|}{|\overrightarrow{AB}|•|\overrightarrow{DC}|}$=$\frac{\frac{6}{2}}{\sqrt{5}×\sqrt{6}}$=$\frac{\sqrt{30}}{10}$，
∴sinθ=$\sqrt{1-（\frac{\sqrt{30}}{10}）^{2}}$=$\frac{\sqrt{70}}{10}$，
∴异面直线DC，AB所成角的正切值tanθ=$\frac{\frac{\sqrt{70}}{10}}{\frac{\sqrt{30}}{10}}$=$\frac{\sqrt{21}}{3}$．
故选：D．
点评 本题考查异面直线所成角的正切值的求法，是基础题，解题时要认真审题，注意向量法的合理运用．
如图是我校100名高三学生第6次月考考试数学成绩的频率分布直方图，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．（1）求图中a的值和这100名学生数学成绩的平均数；
（2）若这100名学生数学成绩某些分数段的人数（x）与地理成绩相应分数段的人数（y）之比如表所示，求地理成绩在[50，90）之外的人数．
| 分数段 | [50，60） | [60，70） | [70，80） | [80，90） |
| x：y | 1：1 | 2：1 | 3：4 | 4：5 |
| A． | 若3a+2a=3b+3b，则a＜b | B． | 若3a+2a=3b+3b，则a＞b | ||
| C． | 若3a-2a=3b-3b，则a＜b | D． | 若3a-2a=3b-3b，则a＞b |
如图，在直角梯形ABCD中，AB∥DC，AD⊥AB，AD=AB=2，DC=4，点M是梯形ABCD内或边界上的一个动点，点N是DC边的中点，则$\overrightarrow{AM}•\overrightarrow{AN}$的最大值是12．
如图，某景区有一座高AD为1千米的山，山顶A处可供游客观赏日出．坡角∠ACD=30°，在山脚有一条长为10千米的小路BC，且BC与CD垂直，为方便游客，该景区拟在小路BC上找一点M，建造两条直线型公路BM和MA，其中公路BM每千米的造价为30万元，公路MA每千米的造价为60万元．