题目内容
在△ABC中，AB=3，∠A=60°，∠A的平分线AD交BC于点D，
=
+λ
（γ∈R），则|
|=（ ）
| AD |
| 1 |
| 3 |
| AC |
| AB |
| AD |
| A、1 | ||
B、
| ||
| C、3 | ||
D、2
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：取AC的一个三等分点E，满足AE=
AC，作DF平行于AE，则由条件可得四边形AEDF为平行四边形，求得∠AFD=120°，∠FAD=30°，∠FDA=30°，可得△AFD为等腰三角形，AF=DF=
AC，故平行四边形AEDF为菱形．利用余弦定理求得AD、BD、CD的值，再由三角形的内角平分线性质可得
=
，由此求得λ的值，从而得到AD的值．
| 1 |
| 3 |
| 1 |
| 3 |
| AC |
| AB |
| CD |
| BD |
解答：
解：△ABC中，∵AB=3，∠A=60°，∠A的平分线AD交边BC于点D，且
=
+λ
，
取AC的一个三等分点E，满足AE=
AC，作DF平行于AE，则由条件可得四边形AEDF为平行四边形，
∴∠AFD=120°，∠FAD=30°，∠FDA=30°，故△AFD为等腰三角形，∴AF=DF=
AC，故四边形AEDF为菱形．
再由AF=λAB=3λ=DF=
AC，可得 AC=9λ，菱形AEDF的边长为3λ．
△AFD中，由余弦定理可得AD2=（3λ）2+（3λ）2-2•3λ•3λ•cos120°=27λ2，∴AD=3
λ．
△ABD中，由余弦定理可得 BD2=32+27λ2-2×3×3
λ×cos30°=27λ2-27λ+9，∴BD=3
．
△ACD中，由余弦定理可得 CD2=81λ2+27λ2-2×9λ×3
λ×cos30°=27λ2=3
λ．
再由三角形的内角平分线性质可得
=
，即
=
，解得 λ=
，或λ=
（舍去）．
故AD=3
λ=3
×
=2
，
故选D．
解：△ABC中，∵AB=3，∠A=60°，∠A的平分线AD交边BC于点D，且| AD |
| 1 |
| 3 |
| AC |
| AB |
取AC的一个三等分点E，满足AE=
| 1 |
| 3 |
∴∠AFD=120°，∠FAD=30°，∠FDA=30°，故△AFD为等腰三角形，∴AF=DF=
| 1 |
| 3 |
再由AF=λAB=3λ=DF=
| 1 |
| 3 |
△AFD中，由余弦定理可得AD2=（3λ）2+（3λ）2-2•3λ•3λ•cos120°=27λ2，∴AD=3
| 3 |
△ABD中，由余弦定理可得 BD2=32+27λ2-2×3×3
| 3 |
| 3λ2-3λ+1 |
△ACD中，由余弦定理可得 CD2=81λ2+27λ2-2×9λ×3
| 3 |
| 3 |
再由三角形的内角平分线性质可得
| AC |
| AB |
| CD |
| BD |
| 9λ |
| 3 |
3
| ||
3
|
| 2 |
| 3 |
| 1 |
| 3 |
故AD=3
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
故选D．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，余弦定理以及三角形的内角平分线性质应用，求得λ的值，是解题的关键和难点，属于中档题．
练习册系列答案
相关题目
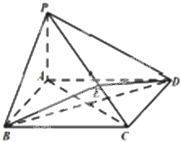如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．PA=1，AD=2．
已知函数f（x）=