题目内容
9.在平面直角坐标系中,直线l的参数方程为$\left\{{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12.(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)已知直线l与曲线C交于A,B两点,试求|AB|.
分析 (Ⅰ)直接由曲线C的极坐标方程求出曲线C的直角坐标方程即可;
(Ⅱ)把直线l的参数方程代入曲线C的方程得5t2+4t-12=0,求出t1+t2和t1t2的值,由此能求出|AB|.
解答 解:(Ⅰ)∵曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12,
∴曲线C的直角坐标方程为3x2+4y2=12,化简得$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)把直线l的参数方程$\left\{{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$代入曲线C的方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,化简整理得5t2+4t-12=0,
∴${t}_{1}+{t}_{2}=-\frac{4}{5}$,${t}_{1}{t}_{2}=-\frac{12}{5}$,
∴|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}=\sqrt{\frac{256}{25}}=\frac{16}{5}$.
点评 本题考查直线的极坐标方程、曲线的直角坐标方程的求法,考查弦长的求法,考查直角坐标方程、极坐标方程、参数方程的互化,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.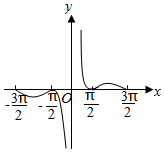 已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
 已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )| A. | $\frac{|cos3x|}{x}$ | B. | $\frac{1+cos2x}{2x}$ | ||
| C. | $\frac{(4{x}^{2}-{π}^{2})(4{x}^{2}-9{π}^{2})}{{x}^{5}}$ | D. | $\frac{|sin2x|}{x}$ |
17.已知实数x,y满足$\left\{\begin{array}{l}{y≥0}\\{x-y≥0}\\{2x-y-2≥0}\end{array}\right.$,则ω=$\frac{y-1}{x+1}$的取值范围是( )
| A. | [-1,$\frac{1}{3}$] | B. | [-$\frac{1}{2}$,$\frac{1}{3}$] | C. | [-$\frac{1}{2}$,1) | D. | [-$\frac{1}{2}$,+∞) |
14.等差数列{an}的前n项和为Sn,若S10=80,a4=5,则a13=( )
| A. | 19 | B. | 21 | C. | 23 | D. | 25 |