Question

20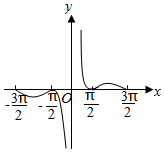．已知函数f（x）的图象如图所示，则f（x）的解析式可能是（　　）

• A． $\frac{|cos3x|}{x}$
• B． $\frac{1+cos2x}{2x}$
• C． $\frac{（4{x}^{2}-{π}^{2}）（4{x}^{2}-9{π}^{2}）}{{x}^{5}}$
• D． $\frac{|sin2x|}{x}$

Answer 1

分析 利用函数的图象特征，检验各个选项中的函数是否满足条件，从而得出结论．

解答 解：由图象可得当x＞0时，f（x）≥0，故可排除C，
因为当$\frac{π}{2}$＜x＜$\frac{3π}{2}$时，f（x）＞0，而当x=π 时，$\frac{|sin2x|}{2x}$=0，不满足图象，故可排除D选项，
又当x=$\frac{5π}{6}$时，$\frac{|cos3x|}{x}$=0，不满足图象，故可排除A选项，
故选：B．

点评 本题主要考查函数的图象特征，属于中档题．