题目内容

设0＜a＜1，实数x，y满足logay-x=0，则关于x的函数y=f（x）的图象是（　　）
A、
B、
C、
D、
考点：指数式与对数式的互化
专题：函数的性质及应用
分析：首先把对数函数转化成指数函数y=ax进一步根据0＜a＜1来确定结果．
解答： 解：实数x，y满足logay-x=0，
则：y=ax，
由于0＜a＜1，
所以函数为减函数．
故选：B．
点评：本题考查的知识要点：对数函数与指数函数的互化，指数函数的单调性．
练习册系列答案
相关题目
直线l：ax+（a+1）y+2=0的倾斜角大于45°，则a的取值范围是
 
．
小明早晨去上学，由于担心迟到被老师批评，所以一开始就跑步，等跑累了再走完余下的路程．如果用纵轴表示小明离学校的距离，横轴表示出发后的时间，则下列四个图形中比较符合小明走法的是哪一个呢？（　　）
A、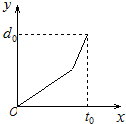
B、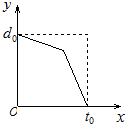
C、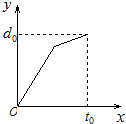
D、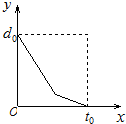
将甲、乙、丙、丁、戊5名大学生分配到3个乡镇去当村官，设事件A为“每个乡镇至少有一名大学生村官”，事件B为“甲、乙、丙三人在同一个乡镇当村官”，则概率P（B|A）等于（　　）
A、
1
25
B、
2
25
C、
1
90
D、
2
81
下列说法中
①
12(-2)4
=
3-2

②
39
=
33

③正数的n次方根有两个      
④a的n次方根就是
na

⑤
nan
=a
⑥(
na
)n=a
正确的个数为（　　）
A、1B、2C、3D、4
已知loga（3a-1）恒为正数，则实数a的取值范围是（　　）
A、(-∞，
1
3
)
B、(
1
3
，
2
3
)
C、（1，+∞）
D、(
1
3
，
2
3
)∪(1，+∞)
设随机变量X～N（1，4），且P（X≤a）=P（X＞2），则实数a的值为（　　）
A、3B、2C、1D、0
在△ABC中，已知sinA+cosA=
1
5
，则△ABC为
 
三角形（在“锐角”、“直角”、“钝角”中，选择恰当的一种填空）．
已知向量
a
=（1+sin2x，sinx-cosx），
b
=（1，sinx+cosx），函数f（x）=
a
•
b
．
（1）求f（x）的最小正周期；
（2）求f（x）的最大值及相应x的值；
（3）若f（θ）=
8
5
，求cos2（
π
4
-2θ）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网