题目内容
5.已知随机变量ξ的分布列为:| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -1 | D. | 1 |
分析 由随机变量ξ的分布列,求出Eξ,再由η=4ξ+3,Eη=4Eξ+3求出η的期望.
解答 解:由随机变量ξ的分布列,知
Eξ=-1×$\frac{1}{2}$+0×$\frac{1}{8}$+1×$\frac{3}{8}$=-$\frac{1}{8}$,
∵η=4ξ+3,
∴Eη=4Eξ+3=4×(-$\frac{1}{8}$)+3=$\frac{5}{2}$.
故选:B.
点评 本题考查了离散型随机变量的数学期望计算问题,是基础题目.

练习册系列答案
相关题目
6.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,$\overrightarrow{a}•\overrightarrow{b}$=1,则向量$\overrightarrow{a}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
15.已知正方形ABCD的边长为1,若在正方形内(包括边界)任取一点M,则△ABM的面积不小于$\frac{1}{8}$的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |
 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD,AB的中点.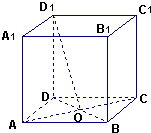 在正方体ABCD-A1B1C1D1中,底面边长为2$\sqrt{2}$,BD与AC交于点O,
在正方体ABCD-A1B1C1D1中,底面边长为2$\sqrt{2}$,BD与AC交于点O,