题目内容
13. 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD,AB的中点.(1)求证:EF∥平面CB1D1;
(2)求CB1与平面CAA1C1所成角的正弦值.
分析 (1)连结BD,由EF∥BD,B1D1∥BD,得EF∥B1D1,由此能证明EF∥平面CB1D1.
(2)设A1C1∩B1D1=O,连结CO,由已知推导出∠B1CO是CB1与平面CAA1C1所成角,由此能求出CB1与平面CAA1C1所成角的大小.
解答  证明:(1)连结BD,
证明:(1)连结BD,
∵在正方体ABCD-A1B1C1D1中,E,F分别为棱AD,AB的中点,
∴EF∥BD,B1D1∥BD,∴EF∥B1D1,
∵EF?平面CB1D1,B1D1?平面CB1D1,
∴EF∥平面CB1D1.
解:(2)设A1C1∩B1D1=O,连结CO,
∵正方体ABCD-A1B1C1D1中,A1B1C1D1是正方形,
∴A1C1⊥B1D1,AA1⊥B1D1,
∵A1C1∩AA1=A1,∴B1O⊥平面CAA1C1,
∴∠B1CO是CB1与平面CAA1C1所成角,
∵OB1=$\frac{1}{2}$CB1,
∴sin∠B1CO=OB1:CB1=$\frac{1}{2}$,
∴CB1与平面CAA1C1所成角的正弦值为$\frac{1}{2}$.
点评 本题考查线面平行的证明,考查直线与平面所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.设向量$\overrightarrow a$,$\overrightarrow b$满足$|\overrightarrow a|=1$,$|\overrightarrow a+\overrightarrow b|=\sqrt{3}$,$\overrightarrow a•(\overrightarrow a+\overrightarrow b)=0$,则$|2\overrightarrow a-\overrightarrow b|$=( )
| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
5.已知随机变量ξ的分布列为:
又变量η=4ξ+3,则η的期望是( )
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -1 | D. | 1 |
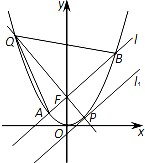 如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.
如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.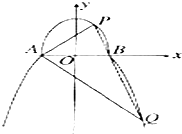 如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.
如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$. 在梯形ABCD中,AD∥BC,∠ABC=90°,AB=a,AD=3a,且∠ADC=arcsin$\frac{{\sqrt{5}}}{5}$,PA⊥平面ABCD,PA=a,则二面角P-CD-A的大小为arctan$\frac{\sqrt{5}}{3}$.
在梯形ABCD中,AD∥BC,∠ABC=90°,AB=a,AD=3a,且∠ADC=arcsin$\frac{{\sqrt{5}}}{5}$,PA⊥平面ABCD,PA=a,则二面角P-CD-A的大小为arctan$\frac{\sqrt{5}}{3}$.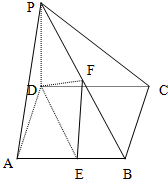 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点