题目内容
6.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,$\overrightarrow{a}•\overrightarrow{b}$=1,则向量$\overrightarrow{a}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
分析 由条件可以求出$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{3}$,$\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{b})=3$,从而根据向量夹角余弦的计算公式即可求出$cos<\overrightarrow{a},\overrightarrow{a}-\overrightarrow{b}>$的值,从而得出向量$\overrightarrow{a}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角.
解答 解:根据条件:
$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{(\overrightarrow{a}-\overrightarrow{b})^{2}}$
=$\sqrt{{\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}$
=$\sqrt{4-2+1}$
=$\sqrt{3}$;
$\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{b})={\overrightarrow{a}}^{2}-\overrightarrow{a}•\overrightarrow{b}=4-1=3$;
∴$cos<\overrightarrow{a},\overrightarrow{a}-\overrightarrow{b}>=\frac{\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}||\overrightarrow{a}-\overrightarrow{b}|}$=$\frac{3}{2\sqrt{3}}=\frac{\sqrt{3}}{2}$;
又$0≤<\overrightarrow{a},\overrightarrow{a}-\overrightarrow{b}>≤π$;
∴$\overrightarrow{a}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角为$\frac{π}{6}$.
故选:A.
点评 考查向量数量积的运算,根据$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{(\overrightarrow{a}-\overrightarrow{b})^{2}}$求$|\overrightarrow{a}-\overrightarrow{b}|$的方法,以及向量夹角的余弦公式,向量夹角的范围.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
| A. | (0,4] | B. | [4,+∞) | C. | (0,2] | D. | [2,+∞) |
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -1 | D. | 1 |
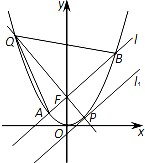 如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.
如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.