题目内容
16.已知z1=1+2i,z2=3-4i,$\frac{1}{z}$=$\frac{1}{z{\;}_{1}}$+$\frac{1}{z{\;}_{2}}$,求z.分析 把z1=1+2i,z2=3-4i代入$\frac{1}{z}$=$\frac{1}{z{\;}_{1}}$+$\frac{1}{z{\;}_{2}}$,然后利用复数代数形式的乘除运算化简得答案.
解答 解:∵z1=1+2i,z2=3-4i,
∴$\frac{1}{z}$=$\frac{1}{z{\;}_{1}}$+$\frac{1}{z{\;}_{2}}$=$\frac{1}{1+2i}+\frac{1}{3-4i}=\frac{1-2i}{(1+2i)(1-2i)}+\frac{3+4i}{(3-4i)(3+4i)}$
=$\frac{1}{5}-\frac{2}{5}i+\frac{3}{25}+\frac{4}{25}i$=$\frac{8}{25}-\frac{6}{25}i$,
∴$z=\frac{1}{\frac{8}{25}-\frac{6}{25}i}=\frac{\frac{8}{25}+\frac{6}{25}i}{(\frac{8}{25}-\frac{6}{25}i)(\frac{8}{25}+\frac{6}{25}i)}$=$2+\frac{3}{2}i$.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
相关题目
11.某几何体的三视图如图所示,则该几何体的表面积是( )
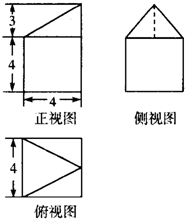

| A. | 98+6$\sqrt{5}$ | B. | 106+6$\sqrt{5}$ | C. | 114+6$\sqrt{5}$ | D. | 106+12$\sqrt{5}$ |
5.已知随机变量ξ的分布列为:
又变量η=4ξ+3,则η的期望是( )
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -1 | D. | 1 |
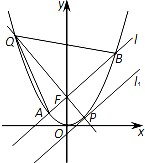 如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.
如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.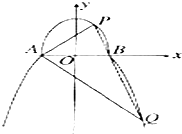 如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.
如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.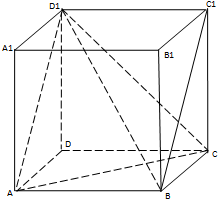 如图在正方体中
如图在正方体中