题目内容
14.(1-x)3(1+x)10的展开式中,x12的系数是-7.分析 根据:(1-x)3(1+x)10=(1-3x+3x2-x3)•(1+${C}_{10}^{1}$x+${C}_{10}^{2}$x2+…+${C}_{10}^{10}$x10),可得展开式中x12的系数.
解答 解:∵(1-x)3(1+x)10=(1-3x+3x2-x3)•(1+${C}_{10}^{1}$x+${C}_{10}^{2}$x2+…+${C}_{10}^{10}$x10),
故展开式中x12的系数为3${C}_{10}^{10}$-${C}_{10}^{9}$=-7,
故答案为:-7.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知随机变量ξ的分布列为:
又变量η=4ξ+3,则η的期望是( )
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -1 | D. | 1 |
9.设随机变量Z的分布列为若$E(Z)=\frac{15}{8}$,则x=$\frac{1}{8}$y=$\frac{3}{8}$
| Z | 1 | 2 | 3 |
| P | 0.5 | x | y |
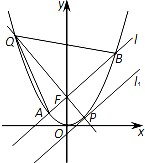 如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.
如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.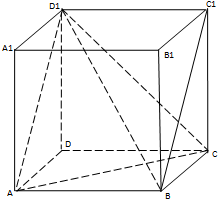 如图在正方体中
如图在正方体中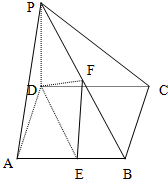 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点