题目内容
15.已知正方形ABCD的边长为1,若在正方形内(包括边界)任取一点M,则△ABM的面积不小于$\frac{1}{8}$的概率是( )| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |
分析 本题是一个等可能事件的概率,以AB为底边,要使面积S≥$\frac{1}{8}$,则三角形的高要h≥$\frac{1}{4}$,高即为p点到AB的距离,得到结果.
解答 解:由题意知本题是一个等可能事件的概率,
以AB为底边,要使面积S≥$\frac{1}{8}$,则三角形的高要h≥$\frac{1}{4}$,高即为p点到AB的距离,
∴概率为$\frac{3}{4}$,
故选:D.
点评 本题考查等可能事件的概率,本题解题的关键是理解三角形的面积的求法.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
5.已知随机变量ξ的分布列为:
又变量η=4ξ+3,则η的期望是( )
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -1 | D. | 1 |
10.已知实数a和b是区间[0,1]内任意两个数,则使b<a2的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
20.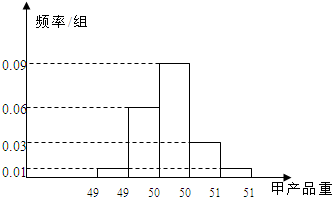 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
已知产品的重量合格标准为:重量值落在(495,510]内的产品为合格品;否则为不合格品.
(1)从甲流水线样本的合格品中任意取2件,求重量值落在(505,510]的产品件数X的分布列;
(2)从乙流水线中任取2件产品,试根据样本估计总体的思想,求其中合格品的件数Y的数学期望;
(3)从甲、乙流水线中各取2件产品,用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”,并用A表示事件“关于x的一元二次方程2x2+2ξx+ξ=0没有实数解”. 试根据样本估计总体的思想,求事件A的概率.
 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:| 乙流水线 产品重量(单位:克) | 频数 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
(1)从甲流水线样本的合格品中任意取2件,求重量值落在(505,510]的产品件数X的分布列;
(2)从乙流水线中任取2件产品,试根据样本估计总体的思想,求其中合格品的件数Y的数学期望;
(3)从甲、乙流水线中各取2件产品,用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”,并用A表示事件“关于x的一元二次方程2x2+2ξx+ξ=0没有实数解”. 试根据样本估计总体的思想,求事件A的概率.
5. 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
 如图在正方体中
如图在正方体中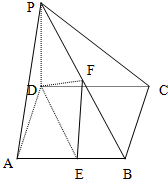 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点