题目内容
20.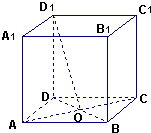 在正方体ABCD-A1B1C1D1中,底面边长为2$\sqrt{2}$,BD与AC交于点O,
在正方体ABCD-A1B1C1D1中,底面边长为2$\sqrt{2}$,BD与AC交于点O,(1)求直线D1O与平面ABCD所成角.
(2)求点D到ACD1的距离.
分析 (1)由题意,∠D1OD是直线D1O与平面ABCD所成角;
(2)过D作DE⊥D1O,则DE⊥平面ACD1,DE为点D到ACD1的距离,利用等面积可得结论.
解答  解:(1)由题意,∠D1OD是直线D1O与平面ABCD所成角,
解:(1)由题意,∠D1OD是直线D1O与平面ABCD所成角,
∵正方体ABCD-A1B1C1D1中,底面边长为2$\sqrt{2}$,
∴DO=2,D1D=2$\sqrt{2}$,
∴tan∠D1OD=$\sqrt{2}$,
∴∠D1OD=arctan$\sqrt{2}$,
∴直线D1O与平面ABCD所成角是arctan$\sqrt{2}$.
(2)过D作DE⊥D1O,则DE⊥平面ACD1,DE为点D到ACD1的距离.
∵DO=2,D1D=2$\sqrt{2}$,D1O=2$\sqrt{3}$,
∴由等面积可得DE=$\frac{2×2\sqrt{2}}{2\sqrt{3}}$=$\frac{2\sqrt{6}}{3}$,
∴点D到ACD1的距离为$\frac{2\sqrt{6}}{3}$.
点评 本题考查线面角,考查点到平面距离的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
11.某几何体的三视图如图所示,则该几何体的表面积是( )
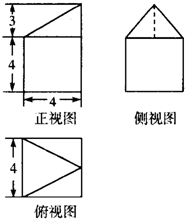

| A. | 98+6$\sqrt{5}$ | B. | 106+6$\sqrt{5}$ | C. | 114+6$\sqrt{5}$ | D. | 106+12$\sqrt{5}$ |
5.已知随机变量ξ的分布列为:
又变量η=4ξ+3,则η的期望是( )
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -1 | D. | 1 |
9.设随机变量Z的分布列为若$E(Z)=\frac{15}{8}$,则x=$\frac{1}{8}$y=$\frac{3}{8}$
| Z | 1 | 2 | 3 |
| P | 0.5 | x | y |
10.已知实数a和b是区间[0,1]内任意两个数,则使b<a2的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |