题目内容
关于x不等式P:x2+﹙a-1﹚x+a2>0与指数函数f(x)=(2a2-a﹚x,若命题“p的解集为R或f(x)在R内是增函数”,是真命题,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:根据题意,求出命题p为真时,a的取值范围,命题q:f(x)在R内是增函数为真时,a的取值范围;
利用p或q为真,得出p和q一真一假,或p、q都为真;从而求出a的取值范围.
利用p或q为真,得出p和q一真一假,或p、q都为真;从而求出a的取值范围.
解答:
解:命题p为真时,一元二次不等式中△=(a-1)2-4a2<0,即a<-1或a>
;
命题q:指数函数f(x)在R内是增函数为真时,2a2-a>1,解得a<-
,或a>1;
∵p或q为真,∴p和q一真一假,或p、q都为真;
当p真q假时,则
,∴
<a≤1;
当p假q真时,则
,∴-1≤a<-
.
p、q都为真;
,∴a<-1,或a>1
综上所述:实数a的取值范围为 {a|a<-
,或a>
}.
| 1 |
| 3 |
命题q:指数函数f(x)在R内是增函数为真时,2a2-a>1,解得a<-
| 1 |
| 2 |
∵p或q为真,∴p和q一真一假,或p、q都为真;
当p真q假时,则
|
| 1 |
| 3 |
当p假q真时,则
|
| 1 |
| 2 |
p、q都为真;
|
综上所述:实数a的取值范围为 {a|a<-
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查了复合命题的真假问题,解题时应根据题意列出正确的不等式组,从而求出答案来,是基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
i是虚数单位,复数z=
的共轭复数
的模为( )
| 2 |
| 1-i |
. |
| z |
| A、1 | ||||
| B、2 | ||||
C、
| ||||
D、
|
已知复数z=
,
是z的共轭复数,则z•
=( )
| ||
1-
|
. |
| z |
. |
| z |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
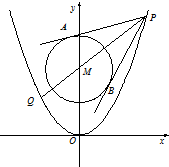 已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为
已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为