题目内容
为了解甲、乙两批次产品中某微量元素的含量,采用随机抽样的方法从两批次产品中各抽取4件,测得它们所含微量元素(单位:毫克)如表:
根据抽样数据推测( )
| 产品编号 | 1 | 2 | 3 | 4 |
| 甲批产品所含微量元素x | 890 | 890 | 850 | 950 |
| 乙批产品所含微量元素y | 900 | 850 | 910 | 920 |
| A、甲批产品所含微量元素比较稳定 |
| B、乙批产品所含微量元素比较稳定 |
| C、两批产品所含微量元素一样稳定 |
| D、以上判断都不对 |
考点:众数、中位数、平均数,极差、方差与标准差
专题:概率与统计
分析:分别求出甲乙的方差,根据方差越小越稳定,判断出结果.
解答:
解:
=
(890+890+850+950)=895,
=
(900+850+910+920)=895
S甲2=
[2×(890-895)2+(850-895)2+(950-895)2]=1275
S乙2=
[(900-895)2+(850-895)2+(910-895)2+(920-895)2]=725
∴S甲2>S乙2
∴乙批产品所含微量元素比较稳定.
故选:B.
. |
| x甲 |
| 1 |
| 4 |
. |
| x乙 |
| 1 |
| 4 |
S甲2=
| 1 |
| 4 |
S乙2=
| 1 |
| 4 |
∴S甲2>S乙2
∴乙批产品所含微量元素比较稳定.
故选:B.
点评:本题主要考查了方差问题,关键是记住方差越小越稳定,越大越不稳定,属于基础题.

练习册系列答案
相关题目
先后抛掷一枚质地均匀的硬币,则两次均正面向上的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
i是虚数单位,复数z=
的共轭复数
的模为( )
| 2 |
| 1-i |
. |
| z |
| A、1 | ||||
| B、2 | ||||
C、
| ||||
D、
|
不等式x2-2x<0的解集是( )
| A、{x|0<x<2} |
| B、{x|0>x>2} |
| C、{x|0<x<2} |
| D、{x|x>0或x<2} |
设集合M={-1,0,1},N={0,1},则M∩N等于( )
| A、{-1,0,1} | B、{0,1} |
| C、{1} | D、{0} |
已知曲线y=x3+ax+b与斜率为2的直线相切于点A(1,3),则b的值为( )
| A、3 | B、-3 | C、5 | D、-5 |
已知复数z=
,
是z的共轭复数,则z•
=( )
| ||
1-
|
. |
| z |
. |
| z |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
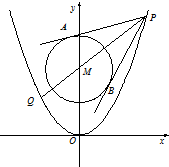 已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为
已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为