题目内容

求函数y=
4x+4
2x
的最小值．
考点：基本不等式
专题：不等式的解法及应用
分析：先化简
4x+4
2x
=2x+
4
2x
，根据指数函数的性质知2x＞0，再根据基本不等式求得最小值．
解答： 解：y=
4x+4
2x
=2x+
4
2x
≥2
2x•
4
2x
=4，当且仅当x=1时取等号．
故函数y=
4x+4
2x
的最小值是4．
点评：本题主要考查了基本不等式的性质，关键是求出等号成立的x的值，属于基础题．
练习册系列答案
相关题目
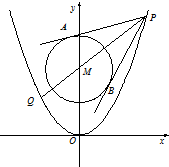已知抛物线C1：x2=2py（p＞0），圆C2：x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为
9
2
，点P是抛物线C1上一点，过点P，M的直线交抛物线C1于另一点Q，且|PM|=2|MQ|，过点P作圆C2的两条切线，切点为A、B．
（Ⅰ）求抛物线C1的方程； 
（Ⅱ）求直线PQ的方程及
PA
•
PB
的值．
画出下列函数的图象
（1）y=x2-2，x∈Z且|x|≤2；
（2）y=-2x2+3x，x∈（0，2）；
 （3）y=
3，x＜-2
-3x，-2≤x＜2
-3，x≥2
．
（Ⅰ）已知0＜θ＜π，sinθ+cosθ=
1
3
，求cos2θ的值；
（Ⅱ）已知-
π
2
＜α＜0＜β＜
π
2
，cos（α-β）=
3
5
，sinβ=
5
13
，求tanα的值．
数列{an}中，已知an=
3
(2n+4)n
，求数列{an}的前n项和Sn．
有甲、乙两个班进行数学考试，按照大于或等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的2×2列联表：
优秀 非优秀 总计
甲班 20
 
 
乙班
 
 60
 
总计
 
 
 210
已知从全部210人中随机抽取1人为优秀的概率为
2
7
．
（1）请完成上面的2×2列联表；
（2）根据列联表的数据，若按99%的可靠性要求，能否认为“成绩与班级有关系”．
附：X2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
，其中n=a+b+c+d
参考数据 当Χ2≤2.706时，无充分证据判定变量A，B有关联，可以认为两变量无关联；
当Χ2＞2.706时，有90%的把握判定变量A，B有关联；
当Χ2＞3.841时，有95%的把握判定变量A，B有关联；
当Χ2＞6.635时，有99%的把握判定变量A，B有关联．
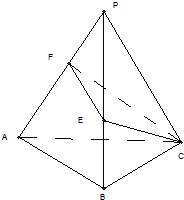如图．P为△ABC所在平面外一点，PA⊥PB，PB⊥PC，PC⊥PA，若PA=
5
PB=
10
PC=2
2
，且点E，F分别在线段PB，PA上满足：PE：EB=1：2，PF：FA=2：3
（Ⅰ）求证：△ABC为锐角三角形； 
（Ⅱ）求多面体ECAB的体积．
在△ABC中，已知sinA=
3
5
，则sin2A的值为
 
．
已知在R上的偶函数f（x）满足f（4-x）=f（x），且当x∈（-1，3]时，f（x）=
x2，x∈(-1，1]
1+cos
1
2
πx，x∈(1，3]
，则g（x）=f（x）-|lgx|的零点数为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网