题目内容
在数列{an}中,a1=64,an+1=
an(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log2an,求数列{|bn|}的前n项和Sn.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)设bn=log2an,求数列{|bn|}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用条件判断数列是等比数列,然后求数列{an}的通项公式;
(2)利用(1)即可求出bn=log2an,然后分段n≤7或n>7求数列{|bn|}的前n项和Sn.
(2)利用(1)即可求出bn=log2an,然后分段n≤7或n>7求数列{|bn|}的前n项和Sn.
解答:
解:(1)∵an+1=
an…1'∴数列{an}成等比数列,且公比 q=
…3'
又a1=64,∴an=64•(
)n-1=27-n…6'
(2)由(1)得:bn=7-n…7'
①当n≤7时,Sn=
=
=
…10'
②当n>7时,Sn=S7-(b8+b9+…+bn)=S7-(Sn-S7)=2S7-Sn=
…13'
| 1 |
| 2 |
| 1 |
| 2 |
又a1=64,∴an=64•(
| 1 |
| 2 |
(2)由(1)得:bn=7-n…7'
①当n≤7时,Sn=
| (b1+bn)•n |
| 2 |
| (6+7-n)•n |
| 2 |
| 13n-n2 |
| 2 |
②当n>7时,Sn=S7-(b8+b9+…+bn)=S7-(Sn-S7)=2S7-Sn=
| n2-13n+84 |
| 2 |
点评:本题考查数列求和,等比数列的殴打与应用,考查计算能力.

练习册系列答案
相关题目
不等式x2-2x<0的解集是( )
| A、{x|0<x<2} |
| B、{x|0>x>2} |
| C、{x|0<x<2} |
| D、{x|x>0或x<2} |
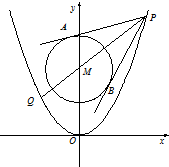 已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为
已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为