题目内容

19．直线y=k（x-1）与A（3，2）、B（0，1）为端点的线段有公共点，则k的取值范围是（　　）
A．[-1，1]B．[-1，3]C．（-∞，-1]∪[3，+∞）D．（-∞，-1]∪[1，+∞）

分析 求出直线y=k（x-1）过定点C（1，0），再求它与两点A（3，2），B（0，1）的斜率，即可取得k的取值范围．

解答 解：y=k（x-1）过C（1，0），
而kAC=$\frac{2-0}{3-1}$=1，kBC=$\frac{1-0}{0-1}$=-1，
故k的范围是（-∞，-1]∪[1，+∞），
故选：D．

点评 本题考查直线的斜率，是基础题．

练习册系列答案
相关题目
4．定积分$\int_{1}^{3}{（2x-\frac{1}{x}）}\;dx$=（　　）
A．10-ln3B．8-ln3C．$\frac{22}{3}$D．$\frac{64}{9}$
5．已知函数f（x）=（x+m）lnx-（m+1+$\frac{1}{e}$）x在x=e处取到极值
（Ⅰ）求m的值
（Ⅱ）当x＞1时，证明f（x）+（2+$\frac{1}{e}$）x＞2x-2
（Ⅲ）如果s，t，r满足|s-r|≤|t-r|，那么称s比t更靠近r，当a≥2且x≥1时，试比较$\frac{e}{x}$和ex-1+a哪个更靠近f（x），并说明理由．
7．设有关于x的一元二次方程x2+2ax+b2=0．
（1）若a是从0，1，2三个数中任取的一个数，b是从0，1，2，3四个数中任取的一个数，求上述方程有实根的概率；
（2）若a是从区间[0，2]任取的一个数，b是从区间[0，3]任取的一个数，求上述方程有实数的概率．
14．已知函数$f（x）=\frac{{{2^x}-a}}{{{2^x}+a}}$是奇函数，其中a∈R，求a的值．
4．定义在R上的函数f（x），满足当x＞0时，f（x）＞1，且对任意的x，y∈R，有f（x+y）=f（x）•f（y），f（2）=3．
（1）求f（0）的值；
（2）求证：对任意x∈R，都有f（x）＞0；
（3）解不等式f（7+2x）＞9．
11．如果函数f（x）=3cos（2x+$\frac{π}{6}$），则f（x）的图象（　　）
A．关于点（-$\frac{π}{12}$，0）对称B．关于点（$\frac{π}{6}$，0）对称
C．关于直线x=$\frac{π}{6}$对称D．关于直线x=$\frac{π}{2}$对称
8．如图是正方体的侧面展开图，l1、l2是两条侧面对角线，则在此正方体中，l1与l2（　　）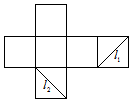
A．互相平行B．相交且夹角为$\frac{π}{3}$C．异面且互相垂直D．异面且夹角为$\frac{π}{3}$
9．在数列{an}中，若a1=-2，且对任意的n∈N*有an+1=1+an，则数列{an}前10项的和为（　　）
A．5B．10C．25D．30

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网