题目内容
19.已知数列{an}是等差数列,前n项和为Sn,若a1=9,S3=21.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若a5,a8,Sk成等比数列,求k的值.
分析 (Ⅰ)利用等差数列前n项和公式求出d=-2,由此能求出数列{an}的通项公式.
(Ⅱ)由a5,a8,Sk成等比数列,得${{a}_{8}}^{2}={a}_{5}•{S}_{k}$,由此能求出k.
解答 解:(Ⅰ)∵数列{an}是等差数列,前n项和为Sn,a1=9,S3=21.
∴${S}_{3}=3×9+\frac{3×2}{2}d=21$,
解得d=-2,
∴an=9+(n-1)×(-2)=-2n+11.
(Ⅱ)∵a5,a8,Sk成等比数列,
∴${{a}_{8}}^{2}={a}_{5}•{S}_{k}$,
即(-2×8+11)2=(-2×5+11)•[9k+$\frac{k(k-1)}{2}×(-2)$],
解得k=5.
点评 本题考查等差数列的通项公式的求法,考查项数k的求法,是基础题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
相关题目
10.已知函数f(x)=lnx,曲线y=g(x)与曲线y=f(x)关于直线y=x对称,若存在一条过原点的直线与曲线y=f(x)和曲线y=g(ax)都相切,则实数a的值为$\frac{1}{e^2}$.
4.定积分$\int_{1}^{3}{(2x-\frac{1}{x})}\;dx$=( )
| A. | 10-ln3 | B. | 8-ln3 | C. | $\frac{22}{3}$ | D. | $\frac{64}{9}$ |
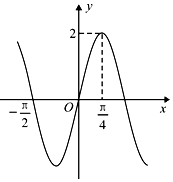 已知函数f(x)=Asin(ωx)(ω>0)的图象如图所示.
已知函数f(x)=Asin(ωx)(ω>0)的图象如图所示.