题目内容
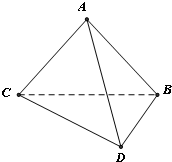 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.(1)证明:平面ADC⊥平面ADB;
(2)求B到平面ADC的距离.
考点:平面与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)由已知得BD⊥面ABC,BD⊥AC,从而AC⊥面ADB,由此能证明面ADC⊥面ADB.
(2)由已知得BD=BC×tan30°=2
,AB=AC=3
,AD=
=
,设B到面ADC的距离为h,由VC-ABD=VB-ACD,能求出B到平面ADC的距离.
(2)由已知得BD=BC×tan30°=2
| 3 |
| 2 |
| AB2+DB2 |
| 30 |
解答:
(本小题满分14分)
(1)证明:∵面ABC⊥面BCD,面ABC∩面BCD=BC,BD?面BCD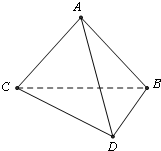 ,
,
∴BD⊥面ABC.(3分)
又AC?面ABC,∴BD⊥AC.(4分)
又AB⊥AC,且BD∩AB=B,
∴AC⊥面ADB.(5分)
又AC?面ADC,∴面ADC⊥面ADB.(6分)
(2)解:在Rt△BCD中,BC=6,∠BCD=30°,
∴BD=BC×tan30°=2
,(7分)
在等腰Rt△ABC中,BC=6,∴AB=AC=3
.(8分)
由(1)知BD⊥面ABC,∴BD⊥AB,(9分)
在Rt△ABD中,AB=3
,DB=2
,
∴AD=
=
,(10分)
又AC⊥面ADB,设B到面ADC的距离为h,
由VC-ABD=VB-ACD,(12分)
得
×
×AB×BD×AC=
×
×AC×AD×h,(13分)
解得h=
,即B到平面ADC的距离为
.(14分)
(1)证明:∵面ABC⊥面BCD,面ABC∩面BCD=BC,BD?面BCD
 ,
,∴BD⊥面ABC.(3分)
又AC?面ABC,∴BD⊥AC.(4分)
又AB⊥AC,且BD∩AB=B,
∴AC⊥面ADB.(5分)
又AC?面ADC,∴面ADC⊥面ADB.(6分)
(2)解:在Rt△BCD中,BC=6,∠BCD=30°,
∴BD=BC×tan30°=2
| 3 |
在等腰Rt△ABC中,BC=6,∴AB=AC=3
| 2 |
由(1)知BD⊥面ABC,∴BD⊥AB,(9分)
在Rt△ABD中,AB=3
| 2 |
| 3 |
∴AD=
| AB2+DB2 |
| 30 |
又AC⊥面ADB,设B到面ADC的距离为h,
由VC-ABD=VB-ACD,(12分)
得
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
解得h=
6
| ||
| 5 |
6
| ||
| 5 |
点评:本题考查平面与平面垂直的证明,考查点到平面的距离的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知函数f(x)=sin(2x-
)(x∈R),下面结论错误的是( )
| π |
| 3 |
| A、函数f(x)的最小正周期为π | ||
B、函数f(x)在区间[0,
| ||
| C、函数f(x)的图象关于直线x=0对称 | ||
D、函数f(x+
|
执行程序框图,输出的结果为( )


| A、9 | B、8 | C、6 | D、4 |
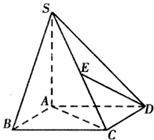 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,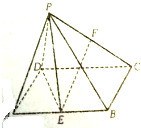 如图,在四棱锥P-ABCD中,底面为矩形ABCD,E,F分别为AB,PC的中点,且PD=PE,PB=PC,求证:
如图,在四棱锥P-ABCD中,底面为矩形ABCD,E,F分别为AB,PC的中点,且PD=PE,PB=PC,求证: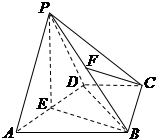 如图,在四棱锥P-ABCD中,侧面PAD是等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB的中点.
如图,在四棱锥P-ABCD中,侧面PAD是等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB的中点.