题目内容
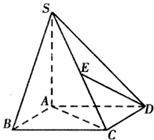 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,E是SC的中点.
(Ⅰ)求异面直线DE与AC所成角;
(Ⅱ)求二面角B-SC-D的大小.
考点:二面角的平面角及求法,异面直线及其所成的角
专题:空间角
分析:(Ⅰ)以点A为坐标原点,AB,AD,AS所在的直线分别为x,y,z轴,建立空间直角坐标系,求出异面直线DE与AC对应的向量,利用向量的数量积求解即可;
(Ⅱ)求出平面BSC的法向量,平面SCD的法向量,利用向量的数量积求二面角B-SC-D的大小.
(Ⅱ)求出平面BSC的法向量,平面SCD的法向量,利用向量的数量积求二面角B-SC-D的大小.
解答:
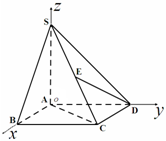 解:(Ⅰ)SA⊥底面ABCD,所以SA⊥AD,SA⊥AB
解:(Ⅰ)SA⊥底面ABCD,所以SA⊥AD,SA⊥AB
底面ABCD是正方形,所以AB⊥AD…(2分)
以点A为坐标原点,AB,AD,AS所在的直线分别为x,y,z轴,建立空间直角坐标系,则A(0,0,0),B(2,0,0),S(0,0,2),C(2,2,0),D(0,2,0),E(1,1,1)…(4分)
所以
=(1,-1,1),
=(2,2,0),
•
=0
所以异面直线DE与AC所成角为90°.…(6分)
(Ⅱ)由题意可知,
=(2,0,-2),
=(2,2,-2)
设平面BSC的法向量为
=(x1,y1,z1),则
,
令z1=1,则
=(1,0,1),…(8分)
=(0,-2,2),
=(2,0,0)
设平面SCD的法向量为
=(x2,y2,z2),则
,
令y2=1,则
=(0,1,1)…(10分)
设二面角B-SC-D的平面角为α,则|cosα|=
=
=
.
显然二面角B-SC-D的平面角为α为钝角,所以α=120°
即二面角B-SC-D的大小为120°.…(12分)
 解:(Ⅰ)SA⊥底面ABCD,所以SA⊥AD,SA⊥AB
解:(Ⅰ)SA⊥底面ABCD,所以SA⊥AD,SA⊥AB底面ABCD是正方形,所以AB⊥AD…(2分)
以点A为坐标原点,AB,AD,AS所在的直线分别为x,y,z轴,建立空间直角坐标系,则A(0,0,0),B(2,0,0),S(0,0,2),C(2,2,0),D(0,2,0),E(1,1,1)…(4分)
所以
| DE |
| AC |
| DE |
| AC |
所以异面直线DE与AC所成角为90°.…(6分)
(Ⅱ)由题意可知,
| SB |
| SC |
设平面BSC的法向量为
| n1 |
|
令z1=1,则
| n1 |
| DS |
| DC |
设平面SCD的法向量为
| n2 |
|
令y2=1,则
| n2 |
设二面角B-SC-D的平面角为α,则|cosα|=
|
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
显然二面角B-SC-D的平面角为α为钝角,所以α=120°
即二面角B-SC-D的大小为120°.…(12分)
点评:本题考查空间向量数量积的应用,二面角以及异面直线所成角的求法,考查计算能力.

练习册系列答案
相关题目
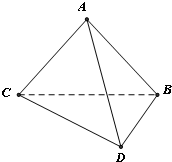 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.