题目内容
化简：
= ．
| cos2x |
| 1-sin2x |
考点：三角函数的化简求值
专题：计算题,三角函数的求值
分析：由条件利用两角和的余弦公式、二倍角公式，求得所给式子的值．
解答：
解：
=
=
=
=
=tan（45°+x）．
故答案为：tan（45°+x）．
| cos2x |
| 1-sin2x |
| cos2x-sin2x |
| (cosx-sinx)2 |
| (cosx-sinx)(cosx+sinx) |
| (cosx-sinx)2 |
| cosx+sinx |
| cosx-sinx |
| 1+tanx |
| 1-tanx |
故答案为：tan（45°+x）．
点评：本题主要考查两角和的余弦公式、二倍角公式的应用，属于基础题．
练习册系列答案
相关题目
设集合S={x|x＞2}，T={x|x2-x-12≤0}，则S∩T=（ ）
| A、[3，+∞） |
| B、[4，+∞） |
| C、（2，3] |
| D、（2，4] |
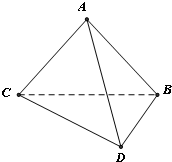如图，将一副三角板拼接，使他们有公共边BC，且使这两个三角形所在的平面互相垂直，∠BAC=∠CBD=90°，AB=AC，∠BCD=30°，BC=6．