已知函数f.下列命题错误的是( )A．不论ϕ取何值.函数f(x)的周期都是πB．存在常数ϕ.使得函数f(x)是偶函数C．不论ϕ取何值.函数f(x)在区间[$π-\frac{ϕ}{2}.\frac{3π}{2}-\frac{ϕ}{2}$]都是减函数D．函数f(x)的图象.可由函数y=cos2x的图象向右平移题目和参考答案——青夏教育精英家教网—

题目内容

14．已知函数f（x）=cos（2x+ϕ）（ϕ＞0且为常数），下列命题错误的是（　　）

	A．	不论ϕ取何值，函数f（x）的周期都是π
	B．	存在常数ϕ，使得函数f（x）是偶函数
	C．	不论ϕ取何值，函数f（x）在区间[$π-\frac{ϕ}{2}，\frac{3π}{2}-\frac{ϕ}{2}$]都是减函数
	D．	函数f（x）的图象，可由函数y=cos2x的图象向右平移ϕ个单位得到

分析 A，周期只与x的系数有关；
B，当ϕ=kπ时，函数f（x）是偶函数；
C，由2kπ≤2x+ϕ≤2kπ+π可得函数f（x）在区间：[kπ-$\frac{ϕ}{2}$，kπ+$\frac{π}{2}$-$\frac{ϕ}{2}$]（k∈N）；
D，函数f（x）的图象，可由函数y=cos2x的图象向右平移$\frac{ϕ}{2}$个单位得到；

解答解：对于A，周期只与x的系数有关，故正确；
对于B，当ϕ=kπ时，函数f（x）是偶函数，故正确；
对于C，由2kπ≤2x+ϕ≤2kπ+π可得函数f（x）在区间：[kπ-$\frac{ϕ}{2}$，kπ+$\frac{π}{2}$-$\frac{ϕ}{2}$]（k∈N）递减，故正确；
对于D，函数f（x）的图象，可由函数y=cos2x的图象向右平移$\frac{ϕ}{2}$个单位得到，故错；
故选：D

点评本题考查了三角函数的图象与性质，属于中档题．

练习册系列答案

相关题目

4．

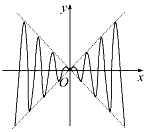如图，虚线部分是平面直角坐标系四个象限的角平分线，实线部分是函数y=f（x）的部分图象，则f（x）可能是（　　）

5．方程x+m=-$\sqrt{4-{x}^{2}}$有且仅有一解，则实数m的取值范围是{-2$\sqrt{2}$}∪（-2，2]．

2．在△ABC中，若cosBcosC-sinBsinC≥0，则这个三角形的形状一定不会是锐角三角形（填“锐角”，或“直角”，或“钝角”）．

9．设x₀是方程lnx+x=4的解，且x₀∈（k，k+1）（k∈Z），求k的值为（　　）

19．设函数f（x）在（m，n）上的导函数为g（x），x∈（m，n），若g（x）的导函数小于零恒成立，则称函数f（x）在（m，n）上为“凸函数”．已知当a≤2时，$f（x）=\frac{1}{6}{x^3}-\frac{1}{2}a{x^2}+x$，在x∈（-1，2）上为“凸函数”，则函数f（x）在（-1，2）上结论正确的是（　　）

	A．	有极大值，没有极小值		B．	没有极大值，有极小值
	C．	既有极大值，也有极小值		D．	既无极大值，也没有极小值

6．与cos50°cos20°+sin50°sin20°相等的是（　　）

3．设△A_nB_nC_n的三边长分别是a_n，b_n，c_n，△A_nB_nC_n的面积为S_n，n∈N^*，若b₁＞c₁，b₁+c₁=2a₁，a_n+1=a_n，b_n+1=$\frac{{{a_n}+{c_n}}}{2}，{c_{n+1}}=\frac{{{a_n}+{b_n}}}{2}$，则（　　）

	A．	{S_n}为递减数列		B．	{S_n}为递增数列
	C．	{S_2n-1}为递增数列，{S_2n}为递减数列		D．	{S_2n-1}为递减数列，{S_2n}为递增数列

5．已知△ABC的三个内角A，B，C成等差数列，若A=45°，AC=4，则△ABC最短边的边长等于（　　）

A．

$\frac{{\sqrt{6}}}{3}$

B．

$\frac{{\sqrt{6}}}{2}$

C．

$\frac{{4\sqrt{6}}}{3}$

D．

$\frac{{\sqrt{3}}}{2}$

试题分类