题目内容
4.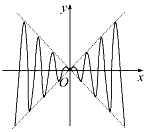 如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )| A. | x2sinx | B. | xsinx | C. | x2cosx | D. | xcosx |
分析 判断函数的奇偶性,结合函数图象的特征,判断函数的解析式即可.
解答 解:由函数的图象可知函数是偶函数,排除选项A,D,
因为x>0时,xsinx≤x恒成立,x2cosx≤x2,即xcosx≤x,x=π时,不等式不成立,
所以C不正确,B正确;
故选:B.
点评 本题考查函数的图象的判断与应用,解析式的判断.

练习册系列答案
相关题目
16.已知命题p:?a∈R,且a>0,a+$\frac{1}{a}$≥2,命题q:?x0∈R,sinx0+cosx0=$\sqrt{3}$,则下列判断正确的是( )
| A. | p是假命题 | B. | q是真命题 | C. | (¬q)是真命题 | D. | (¬p)∧q是真命题 |
13.设函数f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则x•f(x)<0的解集是( )
| A. | {x|-3<x<0或x>3} | B. | {x|x<-3或0<x<3} | C. | {x|x<-3或x>3} | D. | {x|-3<x<0或0<x<3} |
14.已知函数f(x)=cos(2x+ϕ)(ϕ>0且为常数),下列命题错误的是( )
| A. | 不论ϕ取何值,函数f(x)的周期都是π | |
| B. | 存在常数ϕ,使得函数f(x)是偶函数 | |
| C. | 不论ϕ取何值,函数f(x)在区间[$π-\frac{ϕ}{2},\frac{3π}{2}-\frac{ϕ}{2}$]都是减函数 | |
| D. | 函数f(x)的图象,可由函数y=cos2x的图象向右平移ϕ个单位得到 |
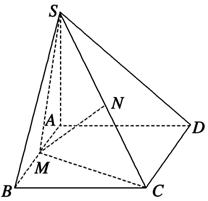 如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.
如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.