题目内容
求函数y=x2-2|x|-1的单调性并证明．
考点：函数单调性的判断与证明
专题：函数的性质及应用,导数的综合应用
分析：根据函数单调性的定义进行证明即可．
解答：
解：∵函数y=x2-2|x|-1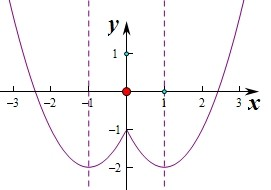
=（|x|-1）2-2为偶函数，
∴作出函数的图象如图：由图象可知函数在x＜-1和0＜x＜1时，函数单调递减，
在x＞1和-1＜x＜0时，函数单调递增．
当x≥0时，y=x2-2|x|-1=x2-2x-1，y'=f'（x）=2x-2，
由f'（x）=2x-2＞0得x＞1，此时函数单调递增，
由f'（x）=2x-2＜0得0＜x＜1，此时函数单调递减，
当x＜0时，y=x2-2|x|-1=x2+2x-1，y'=f'（x）=2x+2，
由f'（x）=2x+2＞0得-1＜x＜0，此时函数单调递增，
由f'（x）=2x+2＜0得x＜-1，此时函数单调递减，
综上：函数的单调递增区间为（-1，0）和（1，+∞），
单调递减区间为（0，1）和（-∞，-1）．
=（|x|-1）2-2为偶函数，∴作出函数的图象如图：由图象可知函数在x＜-1和0＜x＜1时，函数单调递减，
在x＞1和-1＜x＜0时，函数单调递增．
当x≥0时，y=x2-2|x|-1=x2-2x-1，y'=f'（x）=2x-2，
由f'（x）=2x-2＞0得x＞1，此时函数单调递增，
由f'（x）=2x-2＜0得0＜x＜1，此时函数单调递减，
当x＜0时，y=x2-2|x|-1=x2+2x-1，y'=f'（x）=2x+2，
由f'（x）=2x+2＞0得-1＜x＜0，此时函数单调递增，
由f'（x）=2x+2＜0得x＜-1，此时函数单调递减，
综上：函数的单调递增区间为（-1，0）和（1，+∞），
单调递减区间为（0，1）和（-∞，-1）．
点评：本题主要考查二次函数单调性的判断，利用导数是解决函数单调性比较简单的方法．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
如图，四面体ABCD中，O，E分别BD，BC的中点，AB=AD=| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图△ABC为直角三形，