题目内容
若直线y=kx+2与曲线y=
恰有两个不同的交点,则k∈ .
|
考点:直线与圆锥曲线的关系
专题:数形结合,直线与圆,圆锥曲线的定义、性质与方程
分析:作出曲线y=
对应的函数图象,根据图象,即可求出k的取值范围.
|
解答:
 解:曲线y=
解:曲线y=
对应的函数图象如图所示.
当直线y=kx+2与半圆相切时,k=±
满足题意;
当直线y=kx+2过(±1,0)时,k=±2满足题意;
|x|>1时,y=
为双曲线在x轴上方的部分,其渐近线为y=±x.
故当直线y=kx+2与渐近线平行时,k=±1,
∴-1<k<1时,直线与双曲线有两个不同的交点,
∴k∈{k|-1<k<1,或k=±
,或k=±2}.
故答案为:{k|-1<k<1,或k=±
,或k=±2}.
 解:曲线y=
解:曲线y=
|
当直线y=kx+2与半圆相切时,k=±
| 3 |
当直线y=kx+2过(±1,0)时,k=±2满足题意;
|x|>1时,y=
| x2-1 |
故当直线y=kx+2与渐近线平行时,k=±1,
∴-1<k<1时,直线与双曲线有两个不同的交点,
∴k∈{k|-1<k<1,或k=±
| 3 |
故答案为:{k|-1<k<1,或k=±
| 3 |
点评:本题给出动直线与曲线有两个不同的交点,求直线斜率k的取值范围,着重考查了曲线与方程的化简和直线与圆的位置关系,考查数形结合的数学思想等知识,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
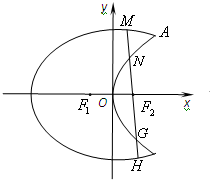 我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆