题目内容
如图，四面体ABCD中，O，E分别BD，BC的中点，AB=AD=| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：点、线、面间的距离计算
专题：计算题,空间位置关系与距离
分析：建立空间直角坐标系，求出平面ACD的法向量，推出EC对应的向量，利用向量的平面上的单位法向量的投影求出距离．
解答：
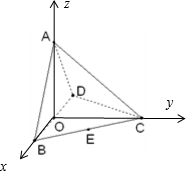解：易证AO⊥平面BCD，以O为原点，OB为x轴，OC为y轴，OA为z轴建立空间直角坐标系，
=(-1，0，-1)，
=(1，
，0)，
设平面ACD的一个法向量：
=(x，y，z)，
则
，即
，不妨令x=-
，则y=1，z=
可求
=(-
，1，
)是平面ACD的一个法向量．
又
=(-
，
，0)，
∴点E到平面ACD的距离h=
=
=
，
故选：B．
解：易证AO⊥平面BCD，以O为原点，OB为x轴，OC为y轴，OA为z轴建立空间直角坐标系，| AD |
| DC |
| 3 |
设平面ACD的一个法向量：
| n |
则
|
|
| 3 |
| 3 |
可求
| n |
| 3 |
| 3 |
又
| EC |
| 1 |
| 2 |
| ||
| 2 |
∴点E到平面ACD的距离h=
|
| ||||
|
|
| ||
|
| ||
| 7 |
故选：B．
点评：本题考查空间点、线、面间的距离计算，求解平面的法向量以及公式的应用是解题的关键．
练习册系列答案
相关题目
如图，某园林单位准备绿化一块直径为BC的半圆形空地，△ABC的地方种草，△ABC的内接正方形PQRS为一水池，其余地方种花，BC=a（a为定值），∠ABC=θ，△ABC的面积为S1，正方形PQRS的面积为S2，当| S1 |
| S2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数中，在区间（0，3）上为增函数的是（ ）
| A、y=-x+1 | ||
| B、y=x2+3 | ||
| C、y=x2-6x+10 | ||
D、y=
|
已知f（x）=3x+3-x，若f（a）=3，则f（2a）等于（ ）
| A、3 | B、5 | C、7 | D、9 |
若sin（π+α）+sin（π-α）+sin（-α）=1，则sinα=（ ）
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |