题目内容
已知函数f(x)=2cos2(x-
)-
cos2x+1,x∈[
,
]
(Ⅰ)求f(x)的最大值和最小值;
(Ⅱ)若对任意实数x,不等式|f(x)-m|<2在x∈[
,
]上恒成立,求实数m的取值范围.
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 2 |
(Ⅰ)求f(x)的最大值和最小值;
(Ⅱ)若对任意实数x,不等式|f(x)-m|<2在x∈[
| π |
| 4 |
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)降幂后利用两角差的正弦函数化积,然后利用x的取值范围求得函数的最大值和最小值;
(Ⅱ)不等式|f(x)-m|<2在x∈[
,
]上恒成立,转化为m-2<f(x)<m+2在x∈[
,
]上恒成立,进一步转化为m-2,m+2与函数f(x)在x∈[
,
]上的最值的关系,列不等式后求得实数m的取值范围.
(Ⅱ)不等式|f(x)-m|<2在x∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解答:
解:(I)f(x)=2cos2(x-
)-
cos2x+1
=cos(2x-
)-
cos2x+2
=sin2x-
cos2x+2
=2(
sin2x-
cos2x)+2
=2(sin2xcos
-cos2xsin
)+2
=2sin(2x-
)+2.
∵x∈[
,
],∴2x-
∈[
,
],
∴当2x-
=
,即x=
时,fmin(x)=3.
当2x-
=
,即x=
时,fmax(x)=4;
(II)|f(x)-m|<2?m-2<f(x)<m+2,
∵对任意实数x,不等式|f(x)-m|<2在x∈[
,
]上恒成立,
∴
,即
,解得:2<m<5.
故m的取值范围为(2,5).
| π |
| 4 |
| 3 |
=cos(2x-
| π |
| 2 |
| 3 |
=sin2x-
| 3 |
=2(
| 1 |
| 2 |
| ||
| 2 |
=2(sin2xcos
| π |
| 3 |
| π |
| 3 |
=2sin(2x-
| π |
| 3 |
∵x∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
∴当2x-
| π |
| 3 |
| π |
| 6 |
| π |
| 4 |
当2x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
(II)|f(x)-m|<2?m-2<f(x)<m+2,
∵对任意实数x,不等式|f(x)-m|<2在x∈[
| π |
| 4 |
| π |
| 2 |
∴
|
|
故m的取值范围为(2,5).
点评:本题考查了三角函数倍角公式,两角差的正弦公式,考查了三角函数最值的求法,考查了数学转化思想方法,关键是把不等式恒成立问题转化为含m的代数式与f(x)的最值关系问题,是中档题.

练习册系列答案
相关题目
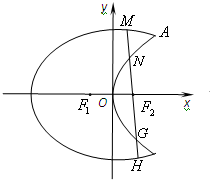 我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆