题目内容
 已知平行六面体ABCD-A1B1C1D1,底面ABCD为菱形,∠BCD=∠C1CD=60°,求:当
已知平行六面体ABCD-A1B1C1D1,底面ABCD为菱形,∠BCD=∠C1CD=60°,求:当| CC1 |
| CD |
考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:当
为1时,能使A1C⊥平面C1BD,A1C与C1O相交于G,说明点G是正三角形C1BD的中心,证明CG⊥平面C1BD,即可证明A1C⊥平面C1BD.
| CC1 |
| CD |
解答:
解:当
为1时,能使A1C⊥平面C1BD.
∵当
为1时,
∴BC=CD=C1C,
又∠BCD=∠C1CB=∠C1CD,
由此可推得BD=C1B=C1D.
∴三棱锥C-C1BD是正三棱锥.(9分)
设A1C与C1O相交于G.
∵A1C1∥AC,且A1C1:OC=2:1,
∴C1G:GO=2:1.
又C1O是正三角形C1BD的BD边上的高和中线,
∴点G是正三角形C1BD的中心,
∴CG⊥平面C1BD,
即A1C⊥平面C1BD.
| CC1 |
| CD |
∵当
| CC1 |
| CD |
∴BC=CD=C1C,
又∠BCD=∠C1CB=∠C1CD,
由此可推得BD=C1B=C1D.
∴三棱锥C-C1BD是正三棱锥.(9分)
设A1C与C1O相交于G.
∵A1C1∥AC,且A1C1:OC=2:1,
∴C1G:GO=2:1.
又C1O是正三角形C1BD的BD边上的高和中线,
∴点G是正三角形C1BD的中心,
∴CG⊥平面C1BD,
即A1C⊥平面C1BD.
点评:本小题主要考查直线与直线、直线与平面的关系,逻辑推理能力,考查空间想象能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若S甲,S乙,S丙分别表示他们测试成绩的标准差,则( )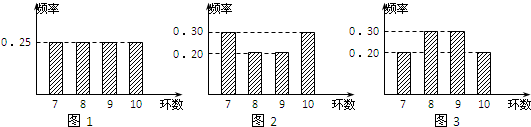

| A、S甲<S乙<S丙 |
| B、S甲<S丙<S乙, |
| C、S乙<S甲<S丙 |
| D、S丙<S甲<S乙 |
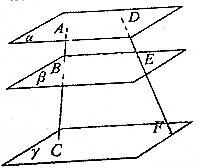 如图,直线AC、DF被三个平行平面α、β、γ所截:
如图,直线AC、DF被三个平行平面α、β、γ所截: