题目内容

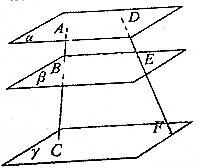如图，直线AC、DF被三个平行平面α、β、γ所截：
（1）是否一定有AD∥BE∥CF；
（2）求证：
AB
BC
=
DE
EF
．
考点：平面与平面平行的判定
专题：空间位置关系与距离
分析：（1）根据直线与平面平行的性质定理，（2）直线与平面平行的性质定理，利用平面内的平行线分线段成比例定理可证．
解答： 解：（1）不一定有AD∥BE∥CF；
∵直线AC∥DF时，三个平行平面α、β、γ，
∴AD∥BE∥CF；
而直线AC、DF是异面直线时，
AD∥BE∥CF不成立，否则与直线AC、DF是异面直线矛盾．
（2）连接AF，交β与O，连接OB，OC，OE，OF，
∵三个平行平面α、β、γ，
∴OB∥OC，OE∥OF，
∴
AB
BC
=
AO
OF
=
DE
EF
．
∴
AB
BC
=
DE
EF
．
点评：本题考查了空间直线与平面的位置关系，平行，垂直关系，属于中档题．
练习册系列答案
相关题目
函数y=(
1
2
)- |x|+1的单调增区间是
 
．
已知p：{x|x2-8x-20≤0}；q：{x|x2-2x-（m2-1）≤0，m＞0}，若非p是非q的必要不充分条件，求实数m的取值范围．
已知命题p：?x0∈（0，2]，使x02-ax0+1＜0，则￢p为（　　）
A、?x0∈（0，2]，使x02-ax0+1≥0
B、?x∈（0，2]，使x2-ax+1＜0
C、?x∈（0，2]，使x2-ax+1≥0
D、?x0∉（0，2]，使x02-ax0+1≥0
如图，在正四棱锥P-ABCD中，底面为正方形，AB=2，VP-ABCD=
4
3
，求异面直线PA、BC所成角的余弦值．
已知向量
a
=（2sinx，2sinx），
b
=（cosx，-sinx），求函数f（x）=
a
•
b
+1．
（1）如果f（x）=
1
2
，求sin4x的值．
（2）如果x∈（0，
π
2
），求f（x）的取值范围．
已知函数f（x）=x2+3|x-a|（a∈R）．若f（x）在[-1，1]上的最小值记为g（a）．
（Ⅰ）求g（a）；
（Ⅱ）证明：当x∈[-1，1]时，恒有f（x）≤g（a）+6．
设 函数f（x）=ax2+bx+1（a≠0，b∈R），若f（-1）=0，且对任意实数x（x∈R）不等式f（x）≥0恒成立．
（1）求实数a、b的值；
（2）在（1）的条件下，当x∈[-2，2]时，g（x）=f（x）-kx是单调函数，求实数k的取值范围．
已知平行六面体ABCD-A1B1C1D1，底面ABCD为菱形，∠BCD=∠C1CD=60°，求：当
CC1
CD
为何值时，有A1C⊥平面C1BD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网