题目内容
1.设变量x,y满足$\left\{\begin{array}{l}{x-y≤10}\\{0≤x+y≤20}\\{0≤y≤15}\end{array}\right.$,则2x+3y的最大值为55.分析 作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.
解答 解:作出不等式$\left\{\begin{array}{l}{x-y≤10}\\{0≤x+y≤20}\\{0≤y≤15}\end{array}\right.$对应的平面区域(阴影部分),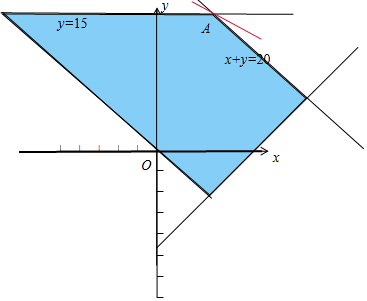
由z=2x+3y,得y=-$\frac{2}{3}$x+$\frac{1}{3}$z.
平移直线y=-$\frac{2}{3}$x+$\frac{1}{3}$z,由图象可知当直线y=-$\frac{2}{3}$x+$\frac{1}{3}$z经过点A时,直线y=-$\frac{2}{3}$x+$\frac{1}{3}$z的截距最大,此时z最大.
由$\left\{\begin{array}{l}{y=15}\\{x+y=20}\end{array}\right.$,解得A(5,15).
此时z的最大值为z=2×5+3×15=55,
故答案为:55.
点评 本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
17.下列说法正确的是( )
| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | a∈R,“$\frac{1}{a}$<1“是“a>1“的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题 |
16.已知实数x,y满足$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{0≤y≤k}\end{array}\right.$,且z=x+y的最大值为6,则(x+5)2+y2的最小值为( )
| A. | 5 | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
13.命题p:?x∈R,tanx>1,命题q:抛物线y=$\frac{1}{3}$x2的焦点到准线的距离为$\frac{1}{6}$,那么下列命题为真命题的是( )
| A. | ¬p | B. | (¬p)∨q | C. | p∧q | D. | p∧(¬q) |
11.在空间,可以确定一个平面的条件是( )
| A. | 两条直线 | B. | 一点和一条直线 | C. | 三个点 | D. | 一个三角形 |
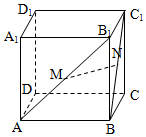 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.