题目内容
6.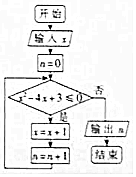 执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )
执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 计算循环中不等式的值,当不等式的值大于0时,不满足判断框的条件,退出循环,输出结果N,再以长度为测度求概率即可.
解答 解:第一次循环,1-4+3=0≤0,x=2,n=1;
第二次循环,-1≤0,x=3,n=2;
第三次循环,0≤0,x=4,n=3;
第四次循环,3>0,不满足条件,
输出n=3,故N=3,
则M≥2,
故满足条件的概率p=$\frac{4-2}{4-(-1)}$=$\frac{2}{5}$,
故选:B.
点评 本题考查循环结构的应用,注意循环的结果的计算,考查计算能力,考查概率的计算,确定N的值是关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
17.下列说法正确的是( )
| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | a∈R,“$\frac{1}{a}$<1“是“a>1“的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题 |
14.已知A是抛物线M:y2=2px(p>0)与圆C在第一象限的公共点,其中圆心C(0,4),点A到M的焦点F的距离与C的半径相等,M上一动点到其准线与到点C的距离之和的最小值等于C的直径,O为坐标原点,则直线OA被圆C所截得的弦长为( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | $\frac{7\sqrt{2}}{6}$ | D. | $\frac{7\sqrt{2}}{3}$ |
1.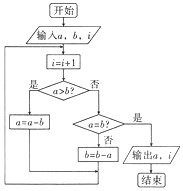 图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
 图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )| A. | 2,5 | B. | 2,4 | C. | 0,4 | D. | 0,5 |