题目内容
15.已知函数$f(x)=mx-\frac{m-1+2e}{x}-lnx$,m∈R,函数$g(x)=\frac{1}{xcosθ}+lnx$在[1,+∞)上为增函数,且θ∈$({-\frac{π}{2},\frac{π}{2}})$.(Ⅰ)当m=0时,求函数f(x)的单调区间和极值;
(Ⅱ)求θ的值;
(Ⅲ)若在[1,e]上至少存在一个x0,使得f(x0)>g(x0)成立,求m的取值范围.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间和极值即可;
(Ⅱ)求出函数的导数,问题转化为xcosθ-1≥0在[1,+∞)上恒成立,根据θ的范围,求出θ的值即可;
(Ⅲ)令$F(x)=f(x)-g(x)=mx-\frac{m+2e}{x}-2lnx$,通过讨论m的范围,求出F(x)的最大值,从而求出m的范围即可.
解答 解:(Ⅰ)∵m=0,∴$f(x)=-\frac{-1+2e}{x}-lnx$,x∈(0,+∞),
∴${f^/}(x)=\frac{2e-1}{x^2}-\frac{1}{x}=\frac{2e-1-x}{x^2}$.
令f′(x)=0,则x=2e-1∈(0,+∞).
∴x,f′(x)和f(x)的变化情况如下表:
| x | (0,2e-1) | 2e-1 | (2e-1,+∞) |
| f′(x) | + | 0 | - |
| f(x) | 递增 | 极大值f(2e-1)=-1-ln(2e-1) | 递减 |
函数f(x)有极大值f(2e-1)=-1-ln(2e-1);
(Ⅱ) 由已知$g'(x)=-\frac{1}{{cosθ•{x^2}}}+\frac{1}{x}≥0$在[1,+∞)上恒成立,
即$\frac{xcosθ-1}{{{x^2}cosθ}}≥0$,∵$θ∈(-\frac{π}{2},\frac{π}{2})$,∴cosθ>0,
故xcosθ-1≥0在[1,+∞)上恒成立,只需1•cosθ-1≥0,
即cosθ≥1,∴只有cosθ=1,$θ∈(-\frac{π}{2},\frac{π}{2})$,知θ=0;
(Ⅲ)令$F(x)=f(x)-g(x)=mx-\frac{m+2e}{x}-2lnx$,
$当m≤0时,由x∈[{1,e}],有mx-\frac{m}{x}≤0,且-2lnx-\frac{2e}{x}<0$,
∴此时不存在x0∈[1,e],使得f(x0)>g(x0)成立;
$当m>0时,F'(x)=m+\frac{m+2e}{x^2}-\frac{2}{x}=\frac{{m{x^2}-2x+m+2e}}{x^2}$.
故F(x)在[1,e]上单调递增,
∴$F{(x)_{max}}=F(e)=me-\frac{m}{e}-4$,
令me-$\frac{m}{e}$-4>0,解得:m>$\frac{4e}{{e}^{2}-1}$,
故所求m的范围是($\frac{4e}{{e}^{2}-1}$,+∞).
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,考查函数恒成立问题,是一道综合题.

练习册系列答案
相关题目
11.设变量x,y满足约束条件$\left\{{\begin{array}{l}{x-y≥-1}\\{x+y≤4}\\{y≥2}\end{array}}\right.$,则目标函数z=x+2y的最大值为( )
| A. | 5 | B. | 6 | C. | $\frac{13}{2}$ | D. | 7 |
3.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-6≤0,}&{\;}\\{x-y-1≤0,}&{\;}\\{x-1≥0.}&{\;}\end{array}\right.$若a∈[-2,9],则z=ax+y仅在点($\frac{7}{3}$,$\frac{4}{3}$)处取得最大值的概率为( )
| A. | $\frac{9}{11}$ | B. | $\frac{7}{11}$ | C. | $\frac{6}{11}$ | D. | $\frac{5}{11}$ |
4.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左焦点为F(-c,0)(c>0),过点F作圆${x^2}+{y^2}=\frac{a^2}{4}$的一条切线交圆于点E,交双曲线右支于点P,若$\overline{OP}=2\overline{OE}-\overline{OF}$,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 2 |
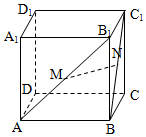 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.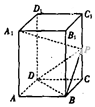 如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.
如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.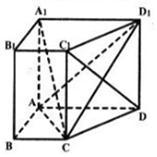 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中