题目内容
12.已知数列{an}满足a1=2,且$\frac{a_1}{2}+\frac{a_2}{3}+\frac{a_3}{4}+…+\frac{{{a_{n-1}}}}{n}={a_n}-2(n≥2)$,则{an}的通项公式为an=n+1.分析 依题意可得$\frac{{a}_{1}}{2}+\frac{{a}_{2}}{3}+\frac{{a}_{3}}{4}+…+\frac{{a}_{n-1}}{n}+\frac{{a}_{n}}{n+1}={a}_{n+1}-2$,与已知关系式作差可得$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+2}{n+1}$,可判断出数列{$\frac{{a}_{n}}{n+1}$}是以1为公比的等比数列,结合题意可知其首项为$\frac{{a}_{1}}{1+1}$=1,利用等比数列的通项公式即可求得答案.
解答 解:∵$\frac{a_1}{2}+\frac{a_2}{3}+\frac{a_3}{4}+…+\frac{{{a_{n-1}}}}{n}={a_n}-2(n≥2)$,①
$\frac{{a}_{1}}{2}+\frac{{a}_{2}}{3}+\frac{{a}_{3}}{4}+…+\frac{{a}_{n-1}}{n}+\frac{{a}_{n}}{n+1}={a}_{n+1}-2$,②
①-②得:$\frac{{a}_{n}}{n+1}$=an+1-an,整理得:$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+2}{n+1}$,
∴$\frac{\frac{{a}_{n+1}}{n+2}}{\frac{{a}_{n}}{n+1}}$=1,又$\frac{{a}_{1}}{1+1}$=1,
∴数列{$\frac{{a}_{n}}{n+1}$}是以1为首项,1为公比的等比数列,
∴an=n+1,
故答案为:an=n+1.
点评 本题考查数列递推式,求得数列{$\frac{{a}_{n}}{n+1}$}是以1为首项,1为公比的等比数列是关键,也是难点,考查推理与运算能力,属于中档题.

| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | 3 | D. | 2 |
| A. | 5 | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | [-1,3) | B. | [0,3) | C. | [1,3) | D. | (1,3) |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{36}$ | D. | $\frac{5}{18}$ |
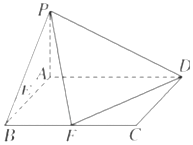 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.