题目内容
17.设复数z满足$\frac{z+1}{z-2}=1-3i$,则|z|=( )| A. | 5 | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 把已知等式变形,利用复数代数形式的乘除运算化简求得z,再由复数模的计算公式得答案.
解答 解:由$\frac{z+1}{z-2}=1-3i$,得z+1=z-2-3i•z+6i,即3i•z=-3+6i,
∴$z=\frac{-3+6i}{3i}=\frac{(-3+6i)(-i)}{-3{i}^{2}}$=$\frac{6+3i}{3}=2+i$,
∴|z|=$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.已知圆C1:x2+y2=4,圆C2:x2+y2+6x-8y+16=0,则圆C1和圆C2的位置关系是( )
| A. | 相离 | B. | 外切 | C. | 相交 | D. | 内切 |
2.某程序框图如图所示,该程序运行后输出的S的值是( )
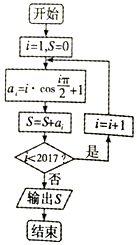

| A. | 1007 | B. | 3025 | C. | 2017 | D. | 3024 |