题目内容
设集合A={x|x2-4x+3＜0}，B={x|x2-2x+a-8≤0}，且A⊆B，求a的取值范围．
考点：集合的包含关系判断及应用
专题：集合
分析：先求出A=（1，3），设f（x）=x2-2x+a-8，容易判断该函数的对称轴在1，3之间，所以要使A⊆B，只要
，所以解该不等式组即得a的取值范围．
|
解答：
解：A=（1，3），设f（x）=x2-2x+a-8；
∵A⊆B，容易判断f（x）的对称轴在区间（1，3）内；
∴
；
解得a≤5；
∴a的取值范围为（-∞，5]．
∵A⊆B，容易判断f（x）的对称轴在区间（1，3）内；
∴
|
解得a≤5；
∴a的取值范围为（-∞，5]．
点评：考查一元二次不等式解的情况，子集的概念，以及二次函数的对称轴．
练习册系列答案
阅读快车系列答案
相关题目
已知a＞0，b＞0，c＞0，且asin2θ+bcos2θ＜c，则（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
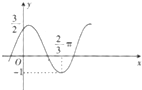将函数y=Asinωx+b（A，ω，b均为正实数）的图象向左平移| π |
| 12 |
A、y=2sin（x+
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
点（-5，1）关于直线x-2y+2=0的对称点是（ ）
| A、（3，3） |
| B、（-3，-3） |
| C、（5，1） |
| D、（5，-1） |
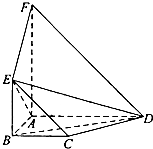如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD=∠FAB=90°，BC