题目内容
已知正实数a，b满足
+
=1，x=a+b，则实数x的取值范围是（ ）
| 2 |
| a |
| 1 |
| b |
| A、[6，+∞） | ||
B、{2
| ||
C、[4
| ||
D、[3+2
|
考点：基本不等式在最值问题中的应用
专题：计算题,不等式的解法及应用
分析：由
+
=1，化简x=a+b=（a+b）（
+
）=2+1+
+
，从而利用基本不等式，注意等号是否能成立．
| 2 |
| a |
| 1 |
| b |
| 2 |
| a |
| 1 |
| b |
| 2b |
| a |
| a |
| b |
解答：
解：∵
+
=1，
∴x=a+b=（a+b）（
+
）=2+1+
+
≥3+2
，
（当且仅当
=
即b=
+1，a=2+
时，等号成立），
故选D．
| 2 |
| a |
| 1 |
| b |
∴x=a+b=（a+b）（
| 2 |
| a |
| 1 |
| b |
| 2b |
| a |
| a |
| b |
| 2 |
（当且仅当
| 2b |
| a |
| a |
| b |
| 2 |
| 2 |
故选D．
点评：本题考查了基本不等式的应用，属于中档题．
练习册系列答案
小题狂做系列答案
相关题目
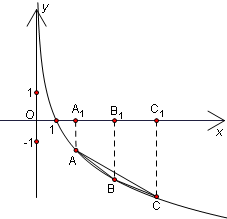如图，A，B，C是函数